

The Genesis of General Relativity
(7) Einstein's 1916 Paper
[(1)//(2)//(3)//(4)//(5)//(6)//(7)//(8)]
The Genesis of General Relativity
(7) Einstein's 1916 Paper: Die Grundlage der allgemeinen Relativitaetstheorie, Annalen der Physik 49 (1916), 769-822.
What happened with Einstein's Nobel Prize? I am not asking "Why was he awarded by his paper on photo-electric effect, rather than by papers on relativity?"; I am asking about the fate of the money! On such worldly matters, Highfield and Carter are informative.
There was similar widespread ignorance about the fate of the Nobel prize money. Einstein received news of his honour in November 1922 as he sailed with Elsa to make a speaking tour of Japan. The money was transferred to Mileva in the following year, but this was kept secret even from Einstein's closest friends. Lorentz, for example, wrote confidently to him that the 'material side' of the prize would 'ease the cares' of his daily life. In fact it was used to buy three houses for Mileva in Zurich: one to live in, the other two as investments. She made her home at Huttenstrasse 62, a five-story house on the Zurichberg. There she lived until her death. ...
Einstein's letters around this time show a genuine rapproachement with his ex-wife, as if the handing over of the Nobel prize money had cleared the air between them. (Highfield & Carter, The Private Lives of Albert Einstein, 221-222)
We have explained, roughly according to the chronological order, most of the major elements of the general theory of relativity. Now it remains to review some of the philosophical arguments in this definitive paper, and to fill out some of the technical details in intuitively manageable terms (for mathematically untrained readers, like myself).
Physical meaning of coordinate systems radically changes
At the end of section 1, Einstein calls our attention to the following feature of the special relativity, formulated in the Minkowski coordinates. Although it has brought some important changes in our view of space and time, it still keeps this conservative element.
Zwei hervorgehobenen materiellen Punkten eines ruhended (starren) Koerpers entspricht hierbei stets eine Strecke von ganz bestimmter Laenge, unabhaengig von Ort und Orientierung des Koerpers sowie von der Zeit; zwei hervorgehobenen Zeigerstellungen einer relativ zum (berechtigten) Bezugssystem ruhenden Uhr entrpricht stets eine Zeitstrecke von bestimmter Laenge, unabhaengig von Ort und Zeit. Es wird sich bald zeigen, dass die allgemeine Relativitatstheorie an dieser einfachen physikalischen Deutung von Raum und Zeit nicht festhalten kann. (770)
Since the special relativity is restricted to inertial systems, it says nothing about accelerated systems or systems with gravitational fields; and Einstein is warning the reader that the metric feature of the Minkowski space must be radically changed. Reading a coordinate value, for each coordinate axis, may not give you a measurement of distance or time, so that we may come to a radically new view of coordinate systems, and hence a new view of spacetime expressed by them. We already had a glimpse of this, but we will shortly illustrate this with a simple example.
General Relativity mixed with others
Section 2 states the grounds for extending the postulate of relativity (we already discussed this in gen.relativity.html), and Einstein's claim is mainly philosophical. Referring to classic explanations for the occurrence of inertial forces (by acceleration; e.g., Newton's bucket and the like, as well as Mach's criticism), Einstein takes sides with the Machian view that the cause must not be a mere factitious cause (bloss fingierte Ursache, like the absolute space) but an observable fact (beobachtbare Erfahrungstatsache). Referring to Einstein's own example of two globes (S1 and S2) in a relative rotation around a common axis, he continues as follows:
Das aus S1 und S2 bestehende physikalische System zeigt fuer sich allein keine denkbare Ursache, auf welche das verschiedene Verhalten von S1 und S2 zurueckgefuehrt werden koennte. Die Ursache muss also ausserhalb dieses Systems liegen. Man gelangt zu der Auffassung, dass die allgemeinen Bewegungsgesetze, we;che im speziellen die Gestalten von S1 und S2 bestimmen, derart sein muessen, dass das mechanische Verhalten von S1 und S2 ganz wesentlich durch ferne Massen mitbedingt werden muss, welche wir nicht zu dem betrachteten System gerechnet hatten. Diese fernen Massen (und ihre Relativbewegungen gegen die betrachteten Koerper) sind dann als Traeger prinzipiell beobachtbarer Ursachen fuer das verschiedene Verhalten unserer betrachteten Koerper anzusehen; sie uebernehmen die Rolle der fingierten Ursache R1 [i.e. absolute space]. Von allen denkbaren, relativ zueinander beliebig bewegten Raeumen R1, R2 usw. darf a priori keiner als bevorzugt angesehen werden, wenn nicht der dargelegte erkenntnistheoretische Einwand wieder aufleben soll. Die Gesetze der Physik muessen so beschaffen sein, dass sie in bezug auf beliebig bewegte Bezugssysteme gelten. Wir gelangen also auf diesem Wege zu einer Erweiterung des Relativitaetspostulates. (772)
This passage seems to contain several different lines of argument, and the connection among them are not clear. First of all, the main conclusion Einstein wishes to draw is obvious enough, and that's the italicized part toward the end of the paragraph. But it is one thing to assert this generalized principle of relativity (physical laws must be the same for any reference system), and it is quite another to subscribe to the Machian strategy for explaining the occurrence of inertial forces, even given Einstein's adherence to the equivalence principle. Further, another confusion is introduced by Einstein in the next section 3, when he equates the relativity principle with the requirement of general covariance (roughly, an arbitrary coordinate transformation is allowed, but the same law is preserved through the transformation).
Surely the Newtonian and the special relativistic views give a special status (in some important sense) to inertial systems (with a uniform movement), but with hindsight we can clearly see that one can give a generally covariant formulation even to these theories!
The point is, it is one thing that the physical law envisaged by a theory has some invariant characteristics (e.g., a spatial distance is invariant in the Newtonian theory), and it is quite another to give a generally covariant formulation for that theory, keeping that invariance intact. But in order to illustrate this point, we have to grasp the notion of general covariance.
General Covariance
Section 3 introduces the requirement of general covariance. The historical fact that the general relativity is the first theory which satisfied this requirement led, even a genius of Einstein's rank, to confound "general covariance" with "general relativity".
Einstein first comes back to his initial warning that our traditional view of coordinate systems must be changed in general relativity. And the example he uses is an inertial system (without gravitational field) K and a rotating system K' sharing the origin and the z-axis; thus K' is rotating around the origin on the x-y plane. Suppose one measures the circumference of the same circle (its center is the common origin of K and K') both from K and from K' (see figure).
The observer on K naturally concludes that the renowned ratio is identical with °ë; but the observer on K' would conclude that the ratio is greater than °ë (because the rods along the circumference shrinks, giving a greater value for the circumference; see Einstein on Geometry), thus claiming that the geometry on K' is non-Euclidean! Thus, in order to have a consistent way for dealing with this situation, we have to abandon the traditional view of the relation between measurements and a coordinate system (in which the measurements are made). And the requirement Einstein proposes is this:
Es bleibt daher nichts anderes uebrig, als alle denkbaren Koordinatensysteme als fuer die Naturbeschreibung prinzipiell gleich berechtigt anzusehen. Dies kommt auf die Forderung hinaus:
Die allgemeinen Naturgesetze sind durch Gleichungen auszudruecken, die fuer alle Koordinatensysteme gelten, e.h. die beliebigen Substitutionen gegenueber kovariant (allgemein kovariant) sind.
Es ist klar, dass eine Physik, welche diesem postulat genuegt, dem allgemeinen Relativitaetspostulat gerecht wird. (776)
Now, the italicized paragraph states the requirement of general covariance, but there remains some ambiguity: what does "equations valid for all coordinate systems" mean? If we try to spell this out, then Einstein's last claim that "physics satisfying this postulate is adapted to general relativity" becomes dubious, to say the least.
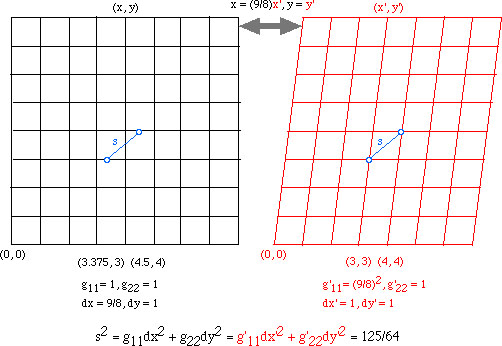
You can see this easily, with the following figure which illustrates a covariant formulation of Euclidean plane geometry and a use of metric tensor gmn in it. In the follwing figure, the black system (x, y) and the red system (x', y') share the same origin, and the two are related by a linear transformation.
ª@
ª@
The point is, a physical theory of Euclidean plane can be formulated in accordance with the requirement of general covariance (coordinate transformation may be arbitrary, although only a linear transformation is used in the figure); and what makes it Euclidean is, among others, that it preserves "distance" as an invariant quantity, and this can be accomplished by the combination of a coordinate transformation and a choice of metric tensor gmn. You do not have to stick to a Cartesian coordinate system, in order to construct an Euclidean theory.
The distance s (shown in blue) is calculated according to Einstein's formula for "line element" (gmn are all zero except for those shown in the figure); given metric tensor as in the figure, the quantity is the same in both systems (thus s is invariant). Although we do not need metric tensor in the usual or standard formulation of Euclidean geometry, a generally covariant formulation will need it; and notice that, in the red coordinate system, the coordinate values and the measurement of s are not as simply related as in the black coordinate system (where the Pythagorean theorem holds directly in terms of coordinate values)!
Likewise, we can give a generally covariant formulation for the Newtonian mechanics and the special relativity too, with appropriate modifications. This clearly shows that the notion of general covariance is completely independent of "relativity", whatever it may mean. However, needless to say, these problems do not detract anything from Einstein's great accomplishment as a scientific work. We have to be careful, not to repeat similar confusions in the name of Einstein's idea.
For further discussion, see references.
References
Friedman, Michael (1983) Foundations of Space-Time Theories, Princeton University Press, 1983, 204-215.
Norton, John D. (1992) "Philosophy of Space and Time", in M. H. Salmon et al, Introduction to the Philosophy of Science, Prentice Hall, 1992, 194-222.
August 31, 2000; last modified, March 28, 2003. (c) Soshichi Uchii