

The Genesis of General Relativity
(4) Einstein's "Hole Argument" in his 1914 Paper
[(1)//(2)//(3)//(4)//(5)//(6)//(7)//(8)]
Why did Einstein think that General Covariance is impossible for the Gravitational Field Equations? Einstein's 1914 Paper: Die formale Grundlage der allgemeinen Relativitaetstheorie, Preussische Akademie der Wissenschaften, Sitzungsberichte (1914), 1030-1085.
It is well known that Einstein, after Einstein & Grossmann paper of 1913, gave up general covariance for the equations of gravitational field. Moreover, he thought that he can offer a "proof" that it is impossible that these equations satisfy the requirement of general covariance, because that would violate another fundamental principle of physics, i.e. the principle of causality; by the latter, he means, roughly in this context, that the stress-energy tensor should uniquely determine the metric tensor. The argument he used for this "proof" is called the "Hole Argument"; it was conceived in late 1913, and was most clearly stated in this 1914 paper. Aside from the original argument, there are a number of good expositions, commentaries, and a development in the recent literature on the history of general relativity and the philosophy of science. My presentation here owes, in particular, to Howard & Norton (1993), Norton (1992), and Stachel (1989); my figure is an adaptation from the figures by Norton in the first two. Incidentally, Pais (1982, 12d) is not particularly helpful on this problem; I would recommend Howard & Norton (1993), for grasping Einstein's original argument and his later "way out".
For typographical reasons I have changed some symbols; so let me briefly state the background of the argument. Einstein and Grossmann (1913) conjectured a correct form of field equations, in which, given the "source" of gravity (stress-energy tensor, here expressed by Tmn), the metric tensor gmn can be determined. Recall that gmn is responsible for the structure of a given spacetime, since it expresses its gravitational field (relative to a given coordinate system K). And the general covariance demands that the law of gravitational field be the same, no matter what coordinate system you may choose for your frame of reference; thus if K' is a system obtained by an arbitrary transformation from the original system K, solutions for the field equations in K' should be as valid as the solutions in K; "solutions" in this context mean, to obtain specific values for gmn or g'mn satisfying the field equations, given the stress-energy tensor Tmn. In the context of the Hole Argument, the stress-energy tensor is the same for both of K and K', because K is so transformed into K' as to fulfill this condition. Now, Einstein argues as follows:
Wir betrachten einen endlichen teil Σ des Kontinuums, in welchem ein materieller Vorgang nicht stattfindet. Das physikalische Geschehen in Σ ist dann vollstaendig bestimmt, wenn in bezug auf ein zur Beschreibung benutztes Koordinatensystem K die Groessen gmn [Greek subscripts in the original] als Funktion der xn [ditto] gegeben werden. Die Gesamtheit dieser Funktionen werde symbolische durch G(x) bezeichnet.
Es werde ein neues Koordinatensystem K' eingefuehrt, welches ausserhalb Σ mit K uebereinstimme, innerhalb Σ aber von K abweiche, derart, dass die auf K' bezogenen g'mn [ditto] wie die gmn (nebst ihren Ableitungen) ueberall stetig sind. Die Gesamtheit der g'mn bezeichnen wir symbolisch durch G'(x'). G(x) und G'(x') beschreiben das naemliche Gravitationsfeld. Ersetzen wir in den Funktionen g'mn die Koordinaten x'n [ditto] durch die Koordinaten xn [ditto], d.h. bilden wir G'(x), so beschreibt G'(x) ebenfalls ein Granvitationsfeld bezueglich K; welches aber nicht uebereinstimmt mit dem tatsaechlichen (bzw. urspruenglich gegebenen) Gravitationsfelde.
Setzen wir nun voraus, dass die Differentialgleichungen des Gravitationsfeldes allgemeinen kovariant sind, so sind sie fuer G'(x') erfuellt (bezueglich K'), wenn sie bezueglich K fuer G(x) erfuellt sind. Sie sind dann also auch bezueglich K fuer G'(x) erfuellt. Bezueglich K existierten dann die voneinander verschiedenen Loesungen G(x) und G'(x), trotzdem an den Gebietsgrenzen beide Loesungen uebereinstimmten, d.h. durch allgemein kovariante Differentialgleichungen fuer das Gravitationsfeld kann das Geschehen in demselben nicht eindeutig festgelegt werden. (1067)
Let us illustrate what Einstein is saying, with the following simple two-dimensional example: In order to help our imagination, we will depict geodesics (which are of course determined by the metric gmn or g'mn), and Einstein's point is that, given the stress-energy tensor, we can have two different geodesics (for instance) within the hole (white region, signified by Σ in Einstein's original), originating from one and converging into one again at the boundaries.
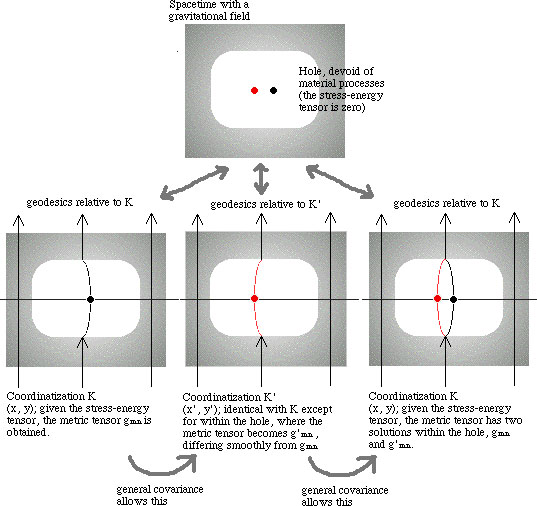
In the Figure, given Tmn, we obtain the first solution gmn in K; then K is transformed into K', thereby the first solution is also transformed into g'mn. Next, in order to obtain the second solution for K, we keep the same functional form (i.e. the coefficients attached to dx, in the Gaussian formula for the line element ds) of g'mn but substitute for its arguments (values of coordinates according to K') the corresponding values according to the original K. Thus, if g'mn has a matrix
1 0
0 -2
at (1, 1) of K', then the second solution in the original K has the same matrix (hence g'mn) at (1, 1) of the original K. That's what is meant by Einstein's statement: "Ersetzen wir in den Funktionen g'mn die Koordinaten x'n durch die Koordinaten xn, d.h. bilden wir G'(x), so beschreibt G'(x) ebenfalls ein Granvitationsfeld bezueglich K". In this way, two geodesics (black and red) within the hole, in the right-most figure, are obtained.
Notice that the two geodesics (black and red) go through a different spacetime point (the black and the red point) respectively in the right-most figure, so that you cannot dismiss the difference between the two solutions as "merely apparent". Thus this "hole argument" raises a serious question as regards the "reality" of spacetime points, and also as regards the "physical meaning" of a coordinate system (for more on this, see Earman 1989, ch. 9 and Norton 1992, 227-230).
Thus, Einstein concludes: if we demand that the course of events in the gravitational field be completely determined by the field equations, we must give up the requirement of general covariance. That was the reason why he felt he lost general covariance; and in the following section (13. Kovarianz bezueglich linearer Transformationen), he elaborates linear transformations which can assure the "uniqueness" within the "hole", where he introduces the notion of "adapted coordinate systems" (angepasste Koordinatensysteme). For the story how he regained general covariance, see Howard & Norton (1993) and Stachel (1989, especially pp. 73-81, 84-88).
References
Earman, J. (1989) World enough and Space-time, MIT Press.
Earman, J., Janssen, M., and Norton, J.D., eds., (1993) The Attraction of Gravitation, Einstein Studies vol. 5, Birkhaeuser.
Howard, D. and Stachel, J., eds. (1989) Einstein and the History of General Relativity, Einstein Studies vol. 1, Birkhaeser.
Howard, D., and Norton, J.D. (1993) "Out of the Labyrinth? Einstein, Hertz, and the Goettingen Answer to the Hole Argument", in Earman et al 1993, pp. 30-62.
Norton, J.D. (1992) "Philosophy of Space and Time" in Salmon, M.H. et al. Introduction to the Philosophy of Science, Prentice Hall, pp.179-231.
Pais, A. (1982) 'Subtle is the Lord ...', Oxford University Press. 邦訳、産業図書、1987。
Stachel, J. (1989) "Einstein's Search for General Covariance, 1912-1915", in Howard &Stachel 1989, pp. 63-100.
August 19, 2000; Last modified March 30, 2003. (c) Soshichi Uchii