

The Genesis of General Relativity
(1) Einstein's 1907 Paper
[(1)//(2)//(3)//(4)//(5)//(6)//(7)//(8)]
Here is a little episode about Einstein and his long-time secretary (1928-1955, and after Einstein's death, became a guardian of his name, together with Otto Nathan) Helen Dukas: "If asked to explain relativity, she would sometimes offer an explanation that he personally devised for her: an hour sitting with a pretty girl passes like a minuite, but a minuite sitting on a hot stove seems like an hour." (Roger Highfield & Paul Carter, The Private Lives of Albert Einstein, St. Martin's Press, 1993, 211)
The Genesis of General Relativity: 1907
Abraham Pais (1982, ch. 9) points out that the basic idea of general relativity occurred to Einstein in 1907 (see Free Fall, quotation from Einstein's manuscript). This idea was stated in the last section V of Einstein's paper "On the relativity principle and the conclusions drawn from it" (1907) which appeared in Jahrbuch der Radioaktivitaet und Elektronik 4 (Original German paper and its English translation in The Collected Papers of Albert Einstein, vol. 2, Princeton; quoations in this article are from the English version). Since this paper is very interesting in that it clearly shows Einstein's way to proceed from the basic idea to some of its specific consequences, it is worthwhile to quote some of its crucial parts (of section V). Unfortunately, this paper is not included in the Japanese translations of slected papers of Einstein, supervised by H. Yukawa; so that it is indeed whorthwhile for Japanese readers!
The section V of this paper begins as follows:
So far we have applied the principle of relativity, i.e., the assumption that the physical laws are independent of the state of motion of the reference system, only to nonaccelerated reference systems. Is it conceivable that the principle of relativity also applies to systems that are accelerated relative to each other? (301)
While this is not the place for a detailed discussion of this question, it will occur to anybody who has been following the applications of the principle of relativity. Therefore I will not refrain from taking a stand on this question here. (302)
Then he introduces the "equivalence principle", without this name yet. He considers two systems °1 and °2 , where the former moves with acceleration Α and the latter is at rest but with homogeneous graviational field, exerting a force equivalent to the acceleration (see my figure, not Einstein's).
As far as we know, the physical laws with respect to °1 do not differ from those with respect to °2 ; this is based on the fact that all bodies are equally accelerated in the gravitational field. At our present state of experience we have thus no reason to assume that the systems °1 and °2 differ from each other in any respect, and in the discussion that follows, we shall therefore assume the complete physical equivalence of a gravitational field and a corresponding acceleration of the reference system. (302)
Incidentally, a uniformly accelerated motion can be represented, in special relativity, by such figures as the following (the worldline is hyperbolic); it may be instructive to imagine how things look like from the reference frame on the red worldline!
With this assumption, Einstein extends his heuristic considerations on gravity, utilizing theoretical treatment of a uniformly accelerated system.
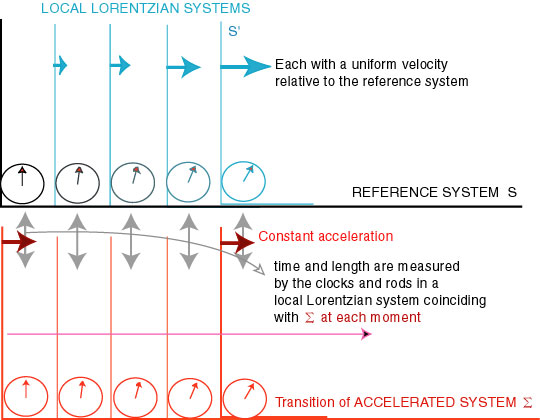
Next he considers a uniformly accelerated system ° relative to a nonaccelerated reference system S (see my figure, not Einstein's). The origin of ° initially coincides with that of S, and the clocks and measuring rods of the two systems are identical; but what will happen with those in °, moving with acceleration Α?
For solving this question, Einstein introduces a third system S' which momentarily coincides with ° at time t' ; this S' is--although Einstein himself does not use this word--a local Lorentzian system moving with a uniform velocity v (obtained by multiplying the acceleration with time), where the special relativity holds. Notice that S' is instantaneously at rest relative to °, but moving with a constant velocity relative to S. And the point is that, (1) the clocks in S and S' are related by Lorentz transformation, and (2) for a short time period, measurements in S' may be used as a substitute for those in °; thus we can define simultaneity and time in ° by employing and combining local Lorentzian systems. The effect of the acceleration on the clocks and rods in ° is negligible; so Einstein argues. For a schematic view of the correspondence between °and the local Lorentzian systems, see the following figure.
@
@
Further, we can compare the relative rates of two clocks situated in two different locations in °. Suppose one location is the origin of ° and the other location is <Μ, 0, 0> on the x-axis (the direction of movement). Then the relation of the time (in approximation) at two points is as in the figure (mine, not Einstein's), and because of the "equivalence principle", the same relation holds in the graviational field (where ³ is the gravitational potential, the difference between <Μ, 0, 0> and <0, 0, 0>. Notice that ³ becomes larger if the distance from the source of gravity is greater).
Now, what does this relation have to do with physics? It means that a clock runs faster at the position where gravitational potential is greater. Thus Einstein predicts the gravitational red shift (the wave length becomes longer, or the frequency becomes smaller).
There exist "clocks" that are present at locations of different gravitational potentials and whose rates can be controlled with great precision; these are the producers of spectral lines. It can be concluded from the aforesaid that the wave length of light coming from the sun's surface, which originates from such a producer, is larger by about one part in two millionth than that of light produced by the same substance on earth. (307)
Notice that if a clock runs faster on the earth (gravitational potential from the sun is larger), the same frequency counted on this clock becomes smaller (thus red shift). Einstein is extending his results obtained in a uniform gravitational field to the case with non-uniform field.
Einstein next proceeds to the effect of gravitation on electromagnetic phenomena. Examining changes in electromagnetic equations (Maxwell equations), he derives an equation which implies the change of the velocity of light in the graviational field (the change of the velocity of light is explicitly announced in his 1911 paper). The velocity (in vacuo) c is replaced by
c(1 + ³/cc)
and from this, he concludes that the path of light (except for those on x-axis) will be bent by the graviational field (310).
Finally, he finds that the principle of conservation of energy still holds, with respect to electromagnetic phenomena, under the "equivalence principle", and concludes that the equivalence of energy E and mass (m~cc) holds not only for the inertial mass but also for the gravitational mass (311).
Thus the major ideas are, it may seem, almost all there in Einstein's 1907 paper. However, he had to spend another eight years for obtaining an adequate equation for gravitational field. Hard mathematics (tensor calculus, Riemanian geometry), and a number of conceptual confusions were waiting for him. To mention only one conspicuous fact, Einstein was, as of 1912, still sticking to the idea of 'flat space', despite he knew that time is 'curved' in an accelerated system (Pais 1982, 11c).
In retrospect, what Einstein tried in this paper may be summarized (in terms of Minkowskian space-time diagram, which may be unknown to Einstein at this point) as follows: He tried in effect to treat the following sort of curved coordinate system (time axis is curved, representing a uniformly accelerated motion). At each point of the time axis, he used a local Lorentzian system having the same velocity at that point (but the Lorentzian system is moving uniformly with that velocity).
By means of the equivalence principle, the following holds:
Most of the basic ideas for general relativity are contained in this figure. However, the idea of "curved space" is absent; this comes only in late 1912. (Added, August 6, 2002)
References
Pais, Abraham (1982) 'Subtle is the Lord ...', Oxford University Press.
The Collected Papers of Albert Einstein, vol. 2 (tr. by Anna Beck and consultant Peter Havas), Princeton University Press, 1989.
Last modified Oct. 9, 2004. (c) Soshichi Uchii