

The Genesis of General Relativity
(2) Einstein's 1911 Paper
[(1)//(2)//(3)//(4)//(5)//(6)//(7)//(8)]
Einstein's 1911 Paper: Ueber den Einfluss der Schwerkraft auf die Ausbreitung des Lichtes, Annalen der Physik 35, 1911, 898-908. Japanese translation by R. Uchiyama, in μGχΔCwACV ^CIWx2A€§A1970A21-32B
In 1911 Einstein moved to Prague, and while in Prague (1911-1912) he published three papers on general relativity. The first is perhaps the most important in that he derived a specific prediction on the deflection of light rays around the sun. And as Pais points out, this paper may be regarded as a direct sequel of Einstein's 1907 paper (written in Bern), because he continues to use the same method of inference and approximation as those of the 1907 paper.
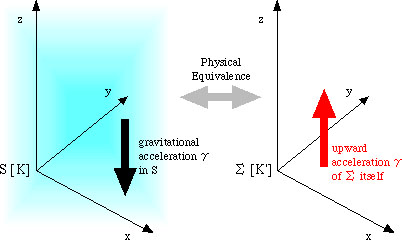
First, in section 1 Einstein states his "equivalence principle" (named "our hypothesis") again, this time taking the direction of the gravitational acceleration as the negative direction of z-axis, as in the figure (mine, not Einstein's); thus the direction of the inertial acceleration must be changed accordingly. Further, he changed the names of the coordinate systems as indicated within the brackets in the figure, but we will retain the old names in the 1907 paper, because the correspondence between the two papers are clearer in this form (thus I will follow Pais in this respect too; Pais 1982, 11b). Local Lorentzian systems --without this name--also appear (so I will use S') in section 2.
Then, Einstein discusses in section 2 the relationship between energy and gravitational mass, in more general terms than those in the 1907 paper (where the question is confined to the electromagnetic phenomena). By reminding the reader of the fact that the special relativity does not tell us anything about gravity, he shows that a significant inference can be made by the "equivalence principle" ("hypothesis").
He presents the following Gedanken-experiment (see the figure; I have freely modified Einstein's original figure): Suppose two physical devices (with identical measuring instruments) are separated h on the z-axis, as in the figure. System S is in a gravitational field, and the gravitational potential at S2 is Αh (i.e. its potential is greater than that at S1 by this amount). Now what is going to happen with energy transmission from S2 to S1 in this gravitational field?
Now, Einstein obtains an answer by the same sort of approximation employed in the 1907 paper, as you can see from the figure. And the relation between E1 and E2 is the same as the one obtained in the 1907 paper, but the consideration leading to this relation is more general. And, by the "equivalence principle", the conclusion obtained for the accelerated system ° can be translated in terms of gravitational potential in the system S. In short, the total energy received at S1 is greater than E2 , but the additional energy amounts to the additional gravitational potential--in other words, gravitational mass--, and the amount is exactly the same as the addition of inertial mass according to the special relativity. Thus the conservation of energy (which remained unsolvable by the special relativity alone, if we take gravity into consideration) can be recovered by the "equivalence principle".
Section 3 (903-906) is devoted to the problem of time in a gravitational field; this section may be rather hard to understand. Einstein now gives an equation of the frequency of the light emitted at S2 and received at S1:
(2) Λ1 = Λ2(1+ (Αh)/cc)
This equation is derived by way of a local Lorentzian system S'--the same method of approximation as that used in his 1907 paper. S' is at rest relative to ° when the light is emitted from S2; thus S1 has a velocity
v =Αh/c
relative to ° when the light is received there. Since we may neglect relativistic effect for such a short process, the classical Dopper effect gives the equation, as an approximation.
Then, by the "equivalence principle", the same effect holds for system S with gravity; we may just replace Αh by gravitational potential ³ at S1 (letting the potential at S2 be 0). And Einstein boldly extends the equation (2a) thus obtained to the case where gravitational field is not uniform.
(2a) Λ1 = Λ2(1+ ³/cc)
With this extension, he obtains the red-shift of the light emitted from the sun and received on the earth. But of course, we need some assumptions about time at each locations.
Einstein asks: Isn't there something absurd in (2) or (2a)? Why is the number of waves--frequency--different at S2 and at S1 when the light comes continually from S2? Einstein's answer is that this absurdity is only apparent.
Wir koennen Λ2 bzw. Λ1 nicht als Frequenzen schlechthin (als anzahl Perioden pro Sekunde) ansehen, da wir eine Zeit im System K [i.e. our S] noch nicht festgelegt haben. Λ2 bedeutet die Anzahl Perioden, bezogen auf die Zeitheit der Uhr U in S2 , Λ2 die Anzahl Perioden, bezogen auf die Zeitheit der gleich beschaffenen Uhr U in S1. Nichts zwingt uns zu der Annahme, dass die in verschiedenen Gravitationspotentialen befindlichen Uhren U also gleich rasch gehend aufgefasst werden muessen. (905)
That is to say, we should not take Λ1 and Λ2 simply as the values of frequency; we still have not determined the time in the accelerated system °or S with gravitation. These two values mean a value measured in terms of the clock at each location; but each clock must have the same property (gleich beschafenen). Whereas nothing forces us to assume that clocks at locations with different potentials run with the same rate, Einstein says. Then how should we measure the time?
Einstein spells out the point as follows:
Dagegen muessen wir die Zeit in K [S] sicher so definieren, dass die Anzahl der Wellenberge und Wellentaler, die sich zwischen S2 und S1 befinden, von dem Absolutwerte der Zeit unabhaengig ist; denn der ins Auge gefasste Prozess ist seiner Natur nach ein stationaerer. Wuerden wie diese Bedingung nicht erfuellen, so kaemen wir zu einer Zeitdefinition, bei deren Anwendung die Zeit explizite in die Naturgesetze einginge, was sicher unnatuerlich und unzweckmaessig waere. Die Uhren in S1 und S2 geben also nicht beide die "Zeit" richtig an. Messen wir die Zeit in S1 mit der Uhr U, so muessen wir die Zeit in S2 mit einer Uhr messen, die 1+³/cc mal langsamer laeuft als die Uhr U, falls sie mit der Uhr U an derselben Stelle vergleichen wird. Denn mit einer solchen Uhr gemessen ist die Frequenz des oben betrachteten Lichtstrahles bei seiner Aussendung in S2 Λ2(1+ ³/cc), also nach (2a) gleich der Frequenz Λ1 desselben Lichtstrahles bei dessen Ankunft in S1. (905-6)
Many different things are said in this condensed passage. First, we have obvious norms for physics, according to which
(i) no law of nature should depend on an absolute value (in other words, a particular position) of time (laws of motion, e.g., do not have such dependence).
From this, it follows that
(ii) the light emitted from S2 and received at S1 must have the same frequency (the number of waves per unit time), whether counted at S2 or at S1.
And the time in the accelerated system ° or gravitational system S should be so defined as to fufill this requirement. And the italicized passage gives the condition for this. But this passage is rather hard and needs more explanation.
Einstein says that if a device emits a light and its frequency is counted on the clock U in the same place, the frequency should be the same, no matter where that device-cum-clock is located (904). But if the locations of emission and reception (counting) are different, counting the frequency at each place (with its local clock U) gives a different value; thus "neither gives the correct time for °". And that's where the italicized passage comes in. Suppose all clocks are made in one location, say at S1, and adjusted to have the same property, including their reading, and then sent to other locations including S2. These clocks are Einstein's U. But these clocks show, despite their initial agreement, a different "time" if their locations have different gravitational potentials; in particular, U at a location with ³ runs at the rate of (1+ ³/cc) relative to U at a location with zero potential. Thus, in order to fulfill the physical norm (2), these "local times" must be adjusted, and for this purpose, a "new" clock must be introduced. Thus
(iii) If we decide to use U where the value of ³ is zero, then a "new" clock must run (1+³/cc)-times slowly than U (if compared at the same location) with variable ³.
That's what the italicized passage says. If you count the frequency of a light at S2 on such a clock, then, for each second on this clock the old U gives (1+³/cc) seconds, so that the frequency counted on this clock becomes identical with the value of (2a). In other words, as Pais points out, a light coming from a location with ³ may be regarded as a clock, because by counting its frequency with a clock U at hand (or the light of the same kind emitted here), you can tell how "the new clock there" works.
All this shows is that a gravitational field affects the rate of local time, so that we need an appropriate adjustment for comparing two events at two locations with different gravitational potentials.
But this has a very important consequence, Einstein continues. That is, if we use the same clock U in order to measure the velocity of light at various locations in ° or in S (with a gravitational field), we will obtain the same value. But, according to the new clock adjusted as in (iii), the velocity of light changes. Letting c be the velocity at the origin of S, the velocity c' at a location with potential ³ is (we have changed symbols for typographical reason):
(3) c' = c(1+ ³/cc)
Thus Einstein reached the same conclusion as that in his 1907 paper, but via a different route.
Note: As regards (i)-(iii), I have utilized and reconstructed the analyses and commentaries by A. Pais (11b, pp. 259-260 of Japanese translation) and by Ryoyu Uchiyama (pp. 29-30 of Uchiyama's tr. of Einstein 1911).
Knowing the complete theory of general relativity, we know that we have to define an appropriate coordinate system(and metric in it) in order to compare local times at different locations; e.g., you may recall Schwarzschild metric, and the distinction between proper time (shell time, etc.) and coordinate time. However, Einstein at this stage still does not have a complete theory and looking for one. See Schwarzschild Geometry.
Finally, in the last section 4, Einstein derives a deflection of light by the gravity of the sun, based on the change of the velocity of light in a gravitational field. See my figure.
@
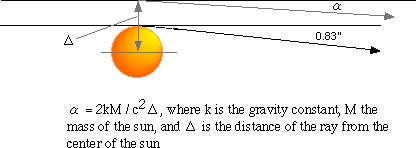
However, this formula (in the figure) and also the specific value 0.83'' turned out to be wrong, because Einstein negelected the change of measuring rods in a gravitational field; the correct formula should be multilied by 2 in the right-hand side. Again, if you know Schwarzschild Geometry, you can easily see where Einstein erred.
References
Pais, Abraham (1982) 'Subtle is the Lord ...', Oxford University Press. Japanese tr., 1987@w_ΝVΰΤΙ΅ΔEEExYΖ}B
The Collected Papers of Albert Einstein, vol. 3 (ed. by M.J.Klein et al., German version with the original pagination), Princeton University Press, 1993.
Last modified March 28, 2003. (c) Soshichi Uchii