

The Genesis of General Relativity
(3) Einstein and Grossmann's 1913 Paper
[(1)//(2)//(3)//(4)//(5)//(6)//(7)//(8)]
Einstein & Grossmann's 1913 Paper: Entwurf einer verallgemeinerten Relativitaetstheorie und einer Theorie der Gravitation, Zeitschrift fuer Mathematik und Physik 62, 1913, 225-261. Also published as an independent book from Teubner, 1913. 邦訳、「一般相対性理論および重力論の草案」(内山龍雄訳)『アインシュタイン選集』2、共立、1970、pp. 33-58。
Einstein came back from Prague to Zuerich in August 1912. Pais conjectures that Einstein realized, around this period, the crucial role of the Riemannian geometry for his new theory of gravity (Pais 1982, 12b). According to Pais's view, (i) Einstein already realized in Prague that the description of a gravitational field in terms of a single gravitational potential (scalar field) must be given up, and (ii) he needed a new geometry but without knowing what sort of geometry it might be. Einstein knew, according to Pais, even that (iii) he needed 10 potentials instead of one, for gravity (the reason for the number "10" will be explained shortly), and that (iv) he was looking for generally covariant equations in order to extend his notion of relativity to accelerated systems; general covariance means, roughly, that a law must have the same form under a general transformation (not just under the Lorentz transformation) of a coordinate system. Moreover, (v) Einstein was aware that the sought-for equation for gravity must be non-linear, because a gravitational field itself becomes a source of the field (Pais, ibid.).
John Stachel's brief description in his article in Twentieth Century Physics vol. 1 (Stachel 1995, 3.2) is also helpful. He points out the importance of Einstein's consideration on the rotating disk; it may well have moved Einstein toward the idea of non-flat spacetime. Stachel argues that this took place in late 1912 (Stachel 1989).
In Zuerich, Einstein began collaboration with Marcel Grossmann (one of Einstein's old friends in ETH), then a professor of mathematics there. Presumably, Einstein asked Grossmann for a help immediately after he came back to Zuerich, and Grossmann came up with the Riemannian geometry and tensor calculus (Grossmann himself was not a specialist in this field). Their 1913 paper is a report on the significant progress (but still in progress) made during this period. It consists of two parts, physical and mathematical, and Einstein is responsible for the first part.
In the introductory part of this paper, Einstein states his "equivalence hypothesis" (now this word appears) for an infinitesimal region; a gravitational field is supposed to be uniform within this small region. Then he refers to Eoetvoes's experimental work on the proportionality of inertial and gravitational mass, as well as to their proportionality in radioactive decay, and defends the plausibility of his hypothesis.
Section 1
For an equation of motion of a mass point (a "free" particle) in a static gravitational field, Einstein now introduces expressions in terms of a Hamiltonian H (if you do not know, consult an elementary textbook on analytic mechanics), and also utilizing a variational principle δ∫ds = 0, where ds is an infinitesimal (Gaussian) "line element" (as you can see shortly). And he reminds the reader of his previous result that the velocity of light c changes depending on a gravitational potential (thus c is closely related with gravitational potential); then the momentum and energy of the mass point contain this variable c in their expressions, and c may now be regarded as a function of spatial coordinates x, y, and z; in other words, c may be taken as a measure for a gravitational potential. Einstein is in effect preparing the ground for an equation for a particle, "freely moving" along a geodesic of the given spacetime with a gravitational field; but for this, we need to know how these geodesics are determined.
In the last paragraph, a reference to Mach appears in relation to the connection of inertial mass with gravitational potential (Einstein thought that his results are in harmony with what he called the "Mach principle", and he tried to pursue this line for a while).
Section 2
Now Einstein tries to show how to generalize the "relativity principle" (of the special relativity), and explains why we need 10 potentials instead of a scalar potential employed in the 1907 and 1911 papers. Suppose we have an arbitrary transformation of coordinates:
x' = x'(x, y, z, t)
y' = y'(x, y, z, t)
z' = z'(x, y, z, t)
t' = t'(x, y, z, t)
And let K' be the new coordinate system (x', y', z', t') and K be the original system (x, y, z, t). Then an infinitesimal interval ds' ("line element", which appeared in the equation of motion in Section 1) is not transformed into as simple a form as is the case with the Lorentz transformation, because the functions x', y' etc. are arbitrary; but ds' has a more general form:
where the coefficients gmn (Einstein's Greek subscripts are changed here) are a function of x', y', z', and t'; and the reason g12, for instance, has 2 in front of it is that g12 and g21are identical (the reason should be clear to anyone familiar with the Gaussian coordinates). The meaning of subscripts of g may become clearer if you replace (x', y', z', t') by
.
The important point to be noticed is that, unlike the case with the special relativity, this interval is not an invariant quantity any more with respect to the Lorentz transformation, and depends on gravitational potentials for the four coordinates (but ds' must be an invariant quantity, because of its physical meaning). The coefficients gmn do precisely the job of expressing this dependency. Let us write down all the coefficient in the following matrix form:
And, as was indicated already, gmn = gnm holds. Then, how many different coefficients (for expressing potentials) remain? Exactly 10, because of the symmetry!
Now, the Minkowski space (which is flat) of the special relativity can be expressed as a special case of the preceding matrix of gmn, as follows:
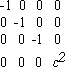
where c is the constant velocity of light in vacuum (this matrix defines the Minkowski metric). Also, the case of a static gravitational field has this form, except that c becomes a function of the first 3 coordinates (thus not a Minkowski space). In modern terminology, gmn is nothing but the metric (tensor), which determines the quantitative relations in a given spacetime; these relations are nothing but an expression of the gravitational field (variable over the points, in general) in the given spacetime. Thus we can see that Einstein has made another breakthrough in his theory.
Section 3
In this section, Einstein explains how to give a physical meaning to coordinates
and ds (the previous "line element" ds' now renamed). Einstein's method is essentially the same as that used in his 1907 and 1911 papers, only more refined: he utilizes local Lorentzian systems for obtaining measurements of coordinates.
Hierzu bemerken wir, dass ds als invariantes Mass fuer den Abstand zweiter unendlich benachbarter Raumzeitpunbkte aufzufassen ist. Es muss daher ds auch eine vom gewaehlten Bezugssystem unabhaengige physikalische Bedeutung zukommen. Wir nehmen an, ds sei der "natuerlich gemessende" Abstand beider Raumzeitpunkte und wollen darunter folgendes verstehen.
Die unmittelbare Nachbarschaft des Punktes
wird bezueglich des Koordinatensystems durch die infinitesimalen Variablen
bestimmt. Wir denken uns statt dieser durch eine lineare Transformation neue Variable
eingefuehrt, ... (Teubner edition, 8)
That is, given a point
,
its neighborhood is determined by
,
so that we may choose (by a certain first order transformation) an appropriate local Lorentzian system (hence no gravity in this) in which
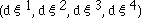
may be substituted for the neighborhood (and the light-cone comes on the main axis). Now, in this Lorentzian system,
and we can measure length and time according to the special relativity; thus if we know the metric gmn which express the gravitational field (or its influence to rods and clocks) around the point, we can know the "naturally measured interval". In the gravitational field, rods and clocks are influenced in a certain way, and how that influence goes is expressed by gmn. In this way, the equivalence hypothesis is now used in an infinitesimal region.
This paper contains a lot more contents, especially a differential equation for gravitational field; but due to a few mistakes, Einstein confessed he could not obtain a general covariant equation for gravitational field; for that, he had to wait until 1915. Since we are going to discuss the completed theory of general relativity according to his 1916 paper "Die Grundlage der allgemeinen Relativitaetstheorie", we will not discuss the rest of this joint paper any further.
References
As regards the history of general relativity, a number of important secondary studies have recently appeared, in addition to primary sources (The Collected Papers of Albert Einstein). In particular, Einstein Studies (The Center for Einstein Studies, Boston University, 9 vols., so far) are important.
Howard, D. and Stachel, J., eds. (1989) Einstein and the History of General Relativity, Einstein Studies vol. 1, Birkhaeser.
Eisenstaedt, J., and Knox, A.J., eds., (1992) Studies in the History of General Relativity, Einstein Studies vol. 3, Birkhaeuser.
Earman, J., Janssen, M., and Norton, J.D., eds., (1993) The Attraction of Gravitation, Einstein Studies vol. 5, Birkhaeuser.
Pais, A. (1982) 'Subtle is the Lord ...', Oxford University Press. 邦訳、産業図書、1987。
Stachel, J. (1989) "The Rigidly Rotating Disk as the 'Missing Link' in the History of General Relativity", in Howard &Stachel, pp. 48-62.
Stachel, J. (1995) Chapter 4, Twentieth Century Physics, vol. 1, Institute of Physics, 1995.
August 16, 2000; Last modified March 28, 2003. (c) Soshichi Uchii