![]()

Avogadro Number and the Brownian Motion
In Mayo's description of Perrin's experiments, the connection of the Brownian motion with the Avogadro number is not clear at all. So I wish to add materials on this extracted from Perrin's own book.
First, we have to notice there is an analogy between gases and dilute solutions: molecules behave quite similarly in a gaseous state and in a dilute solution. And Van't Hoff, starting from this analogy, established the following law (Van't Hoff's Law):
All dissolved substances exert, on a partition that stops them but which allows the solvent to pass, an osmotic pressure equal to the pressure that would be developed in the same volume bu a gaseous substance containing the same number of gramme molecules.
Assuming Avogadro's hypothesis, this is the same as:-- Either as a gas or in solution, the same number of any kind of molecules whatever, enclosed in the same volume at the same temperature, exert the same pressure on the walls that confine them. (Perrin 1990, 39)
Thus, for instance, molecules of different kinds (e.g., hydrogen, helium, and oxygen) would distribute (equilibrium state, gravitation counterbalancing pressure) in huge jars, as in the following figure, provided that the temperature is constant.
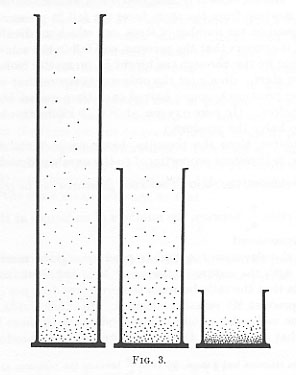
Figure from Perrin (1990), 92 (the largest jar is about 300km. high!).
This shows the effect of the weight of each substance. Then, if we know how much we have to rise in order to find a half of the density of the substance at the bottom, we can calculate the weight of a molecule, and from this we can find the Avogadro number. Now, suppose these laws can be extended to larger particles (such as the Brownian particles) in dilute emulsions.
Is it not conceivable ... that there may be no limit to the size of the atomic asemblages that obey these laws? Is it now conceivable that even visible particles might still obey them accurately, so that a granule agitated by the Brownian movement would count neither more nor less than an ordinary molecule with respect to the effect of its impact upon a partition that stops it? (Perrin 1990, 89)
Then if the answer to this question is affirmative, the same law of the preceding figure can be expected, in a much smaller scale, for tiny particles (tiny, but far larger than a molecule) in a dilute solution, since the density of the solution is much higher than that of any gas. Thus, Perrin concludes:
But if we find that we have only to rise 1/20 millimetre, that is, 100,000,000 times less than in oxygen, before the concentration of the partcles becomes halved, we must conclude that the effective weight of each particle is 100,000,000 times greater than that of an oxygen molecule. We shall thus be able to use the weight of the particle, which is measureable, as an intermediary or connecting link between masses on our usual scale of magnitude and the masses of the molecules. (Perrin 1990, 93-94)
Particles subject to the Brownian motion indeed satisfy such conditions, and Perrin uses Gamboge for this purpose.
I have sought to discover whether the distribution of the grains of radius 0.212ƒÊ ... Cross readings were taken in a cell 100ƒÊ deep on four horizontal equidistant planes across the cell at the levels
5ƒÊ, 35ƒÊ, 65ƒÊ, 95ƒÊ.
The readings gave at these levels, from a count of 13,000 grains, concentrations proportional to the numbers
100, 47, 22.6, 12,
which are approximately equal to the numbers
100, 48, 23, 11.1,
which are in geometrical progression.
... In short, as was expected, the rarefaction law is obeyed exactly. (103)
With these preparations, Perrin is now ready for "weighing molecules" and obtaining the experimental value for the Avogadro number.
Let us consider grains of such a kind that an elevation of 6ƒÊ is sufficient to halve their concentration. To reach the same degree of rarefaction in air, we have seen that a distance of 6 kilometres, which is nearly 10,000 million times as great, is necessary. If our theory is correct, the weight of an air molecule should therefore be one ten thousand-millionth of the weight, in water, of one of the grains. ... and it now only remains to be seen whether numbers obtained by this method are the same as those deduced from the kinetic theory. (104)
And this is the subject of the Step 2 of Perrin's experiments. Actually, Perrin tried four different methods for determining the Avogadro number, and he eventually obtained the following values (multiplied by the 22th power of 10):
68.2, from the vertical distribution of grains (the method here explained)
64, from their translatory displacements (the table is reproduced by Mayo; see How good are Perrin's measurements?)
65, from observations on their rotation
69, from diffusion measurements. (Perrin 1990, 132)
Reference
Perrin, J. (1990) Atoms, Ox Bow Press (reprint).
Last modified Sept. 15, 2007. (c) Soshichi Uchii