

The Genesis of General Relativity
(6) How did Einstein overcome the "Hole" Argument?
Two letters to Paul Ehrenfest, 26 December 1915, and 5 January 1916.
A passage from Einstein 1916: Die Grundlage der allgemeinen Relativitaetstheorie, Annalen der Physik 49 (1916), 769-822.
How did Einstein overcome the "Hole" Argument?
Two letters to Paul Ehrenfest, 26 December 1915, and 5 January 1916.
A passage from Einstein 1916: Die Grundlage der allgemeinen Relativitaetstheorie, Annalen der Physik 49 (1916), 769-822.
ª@
When did Einstein come to the conclusion that he overcame the "Hole Argument", which is the product of his own and once convinced him that the general covariance is impossible for field equations? This is one of the curious problems for historians, and I will leave this for them. Instead, I will discuss the "logic" by which Einstein convinced himself that he can defeat the argument. The documents for my analysis are the two letters to Paul Ehrenfest (already quoted by many people), and a passage from Einstein's 1916 paper.
In the first letter (26 Dec.), he begins his argument with the following amusing "introduction": "Einstein has it easy. Every year he retracts what he wrote in the preceding year; now the sorry business falls to me of justifying my latest retraction." Then he refers to his 1914 paper (Die formale Grundlage).
In ªù12 of my paper of last year, everything is correct (in the first 3 paragraphs) except for what is printed at the end of the third paragraph in spaced type [italicized part in our previous quoation]. A contradiction to the uniqueness of the event does not follow at all from the fact that both systems G(x) and G'(x), related to the same frame of reference, satisify the conditions of the grav. field. The seemingly compelling part of this reflection founders immediately when you consider that
1) the reference system has no real meaning
2) that the (simultaneous) materialization of two different g systems (more aptly put, two different grav. fields) within the same area of the continuum is, according to the nature of the theory, impossible.
In place of ªù12 the following consideration must appear. Whatever is physically real in events in the universe (as opposed to that which is dependent on the choice of a reference system) consist in spatio-temporal coincidences and in nothing else! For ex., the intersection points of two world lines are real, or the statement that they do not intersect each other. Therefore, those statements relating to the physically real do not lose validity from the absence of a (unique) coordinate transformation. When two systems in the gmn's (or gen., the variables used to describe the world) are constituted in such a way that the second can be obtained from the first by mere space-time transformation, then they are entirely equivalent. This is because they have in common all the spatio-temporal point coincidences, that is, all the observables.
This consideration shows simultaneously how natural the requirement of general covariance is. (The Collected Papers, vol. 8, English version, 167)
In this reply, Einstein clearly committs himself to the distinction between the "physically real" and the "mathematical construction", and he is saying that as long as we keep in mind that what is important is the "physically real", the lack of "mathematical uniqueness" does not matter, because if we trace spatio-temporal coincidences (for G(x) and G'(x), for instance), the apparent lack of uniqueness disappears. This argument is known as the "point coincidence" argument.
Thus, in terms of our example of two geodesics within the hole (we will use the same figure), this argument would recover a physical uniqueness as follows:
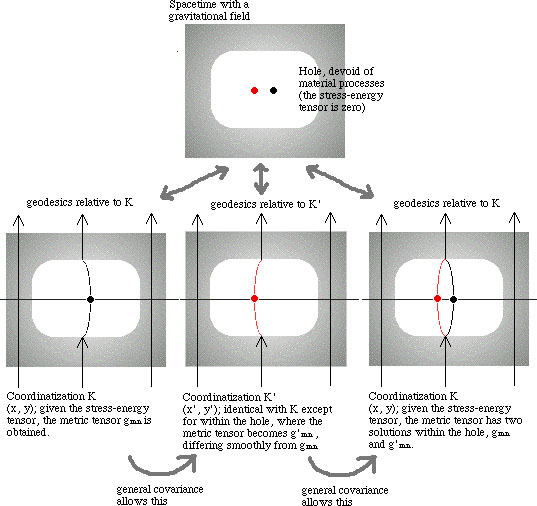
Let us start from the first solution (the black geodesic in the hole in K), and suppose a light traveling along this line intersects a plane of simultaneity, the point of intersection being the black spot on the left-most figure. This point may well be physically real, because it can exemplify a coincidence: then it has a unique counterpart in reality. Next, suppose K is transformed into K', thereby giving the red geodesic in the middle figure. Einstein's point is, then, this red geodesic represents the same solution as the first one, and if the same coincidence as represented by the black spot in K is now transformed into the red spot in K', the two spots merely express the same coincidence (hence the uniqueness is preserved). Finally, if by another covariant transformation this red line becomes the red line in the original coordinate system K, the same argument applies, and hence the second solution, i.e. the red geodesic in the right-most figure, represents the same solution as the first one, and the red spot represents the same coincidence as the black spot does. Thus two solutions are mathematically different, but physically the same, and the physical uniqueness is not lost. The two spots (black and red) in the top figure are misleading; there is in reality only one spot (coincidence). Then, it is obvious that we cannot materialize, within the same continuum, two different solutions gmn and g'mn, but only one, because they are physically the same.
It seems that Ehrenfest was not convinced by this, and asked again by presenting a Gedankenexperiment: suppose light from a distant star passes through a "hole" and then goes through an aperture that directs the light onto a plate; given there are two different solutions, how one can be sure that the light hits the same spot on the plate? (see Figure (a); this is not Einstein's original figure, but no essential points are lost)
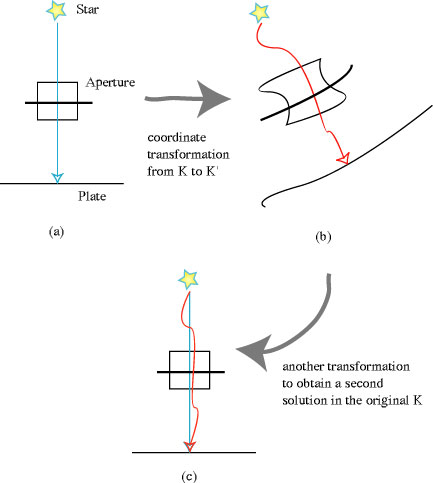
Einstein's reply is his letter of 5 Jan., 1916. In this Einstein's answer is as follows:
I cannot hold it against you that you have not yet understood the admissibility of generally covariant equations, because I myself needed so long to arrive at total clarity on this point. The root of your difficulty lies in that you instinctively treat the reference system as something "real". ... You examine two solutions with the same boundary conditions at infinity, in which the coordinates for the star, the mateiral point at the aperture, and the plate are the same. You ask whether "the direction of the wave normal" at the aperture always comes out the same. As soon as you speak of "the direction of the wave normal at the aperture," you are treating this space with regard to the gmn functions as an infinitesimal space. This and the definiteness of the coordinates for the aperture points have as a consequence that for all solutions the direction of the average waves at the aperture is the same.
Then he immediately adds a finer illustration.
Trace the above little diagram [Figure (a)] on to a completely flexible piece of tracing paper. Then deform the tracing paper ramdomly along the paper plane. Then make another tracing on the letter paper. You then obtain, e.g., the diagram [see Figure (b); this is not Einstein's original figure]
If you now again relate the diagram to orthogonal letter-paper coordinates, the solution is mathematically a different one to beforehand, naturally also with regard to the gmn's. But physically it is exactly the same, simply because the letter-paper coordinate system is only a contrivance. Always the same points are illuminated on the plate. If you perform the distortion of the tracing paper only within the finite realm and in such a way that the image of the star, the aperture, and the plate remain unshifted without damaging the constancy, then you obtain the special case your question refers to.
The essence is this: As long as the drawing paper, i.e., "the space", is unreal, both diagrams do not differ at all. "Coincidences" are what count, e.g., whether the plate points are hit by the light or not. Thus the distinction between your solutions A and B is merely a difference in presentation with physical congruency. (The Collected Papers, vol. 8, English version, 174-5)
All right. This is what Einstein said at the beginning of 1916. I may add a comment on the passage "If you now again relate the diagram to orthogonal letter-paper coordinates". This must mean a construction of the second solution in the original coordinate system, and for the reader's convenience, I have added a third Figure (c), where the red line represents the second solution; but the presumption is that this figure merely shows the case where the starting point of the light and its destination (the spot on the plate) are fixed (in the coordinate system), and two solutions differ smoothly in between. If you wish to insert the three spots of coincidences (the star, the aperture, and the plate), as Einstein suggested, the figure must be modified accordingly.
Now, Einstein's published version of this "point coincidence" argument appears in his 1916 review (Die Grundlage). In section 3, he states the principle of general covariance, and the "coincidence" argument follows:
Die allgemeinhen Naturgesetze sind durch Gleichingen auszudruecken, die fuer alle Koordinatensysteme gelten, d.h. die beliebigen Substitutionen gegenueber kovariant (allgemein kovariant) sind.
Es ist klar, dass eine Physik, welche diesem postulat genuegt, dem allgemeinen Relativitaetspostulat gerecht wird. Denn in allen Substitutionen sind jedenfalls auch diejenigen enthalten, welche allen Relativbewegungen der (dreidimensionalen) Koordinatensysteme entsprechen. Dass diese Forderung der allgemeinen Kovarianz, welche dem Raum und der Zeit den letzten Rest physikalischer Gegenstaendlichkeit nehmen, sine natuerliche Forderung ist, geht aus folgender Ueberlegung hervor. Alle unsere zeitrauemlichen Konstatierungen laufen stets auf die Bestimmung zeitraeumlicher Koinzidenzen hinaus. Bestaende beispielsweise das Geschehen nur in der Bewegung materieller Punkte, so waere letzten Endes nichts beobachtbar als die Begegnungen zweiter oder mehrerer dieser Punkte. Auch die Ergebnisse unserer Messungen sind nichts anderes als die Konstatierung derartiger Bewegungen materieller Punkte unserer Massstaebe mit anderen materiellen Punkten bzw. Koinzidenzen zwischen Uhrzeigern, Zitterblattpunkten und ins Auge gefassten, am gleichen Orte und zur gleichen Zeit stattfindenden Punktereignissen.
Die Einfuehrung einen Bezugssystems dient zu nichts anderem als zur leichteren Beschreibung der Gesamtheit solcher Koinzidenzen. Man ordnet der Welt vier zeitraeumliche Variable
zu, derart, dass jedem Punktereignis ein Wertesystem der Variablen
entspricht. Zwei koinzidierenden Punktereignissen entspricht dasselbe Wertesystem der Variablen
; d.h. die Koinzidenz ist durch die Uebereinstimmung der koordinaten charakterisiert. Fuehrt man statt der Variablen
beliebige Funktionen derselben,
als neues Koordinatensystem ein, so dass die Wertesysteme einander eindeutig zugeordnet sind, so ist die Gleichheit aller vier Koordinaten auch im neuen System der Ausdruck fuer die raumzeitliche Koinzidenz zweiter Punktereignisse. Da sich alle unsere physikalischen Erfahrungen letzten Endes auf solche Koinzidenzen zurueckfuehren lassen, ist zunaechst kein Grund vorhanden, gewisse Koordinatensysteme vor anderen zu bevorzugen, d.h. wir gelangen zu der Forderung der allgemeinen Kovarianz. (776-777)
As regards Einstein's first point, that (1) physics satifying general covariance also satisfies general relativity, we will not discuss here (this seems wrong). We will focus only on coincidence argument. Einstein's second point, that (2) general covariance takes away the last piece of physical objectivity from space and time, is stated quite misleadingly; what he means is that the physical objectivity is taken away from a coordinate system. And then, the coincidence argument comes, first by stating a sweeping claim that (3) all our spatiotemporal verifications reduce to determining spatiotemporal coincidences. After illustrating this point with a few examples, Einstein elaborates (in the third paragraph) his new view on the role of coordinate systems. That is, (4) introducing a reference system is nothing but a means for facilitating our description of the totality of those coincidences. And (5) as long as we keep one-one correspondence when we introduce a new coordinate system, the spatiotemporal identity of two point-events is expressed by the identity of all four coordinate values, respectively. Thus there is no reason to prefer one reference system to another, in conformity with the general covariance.
Incidentally, we can easily imagine how this "coincidence" argument encouraged positivist philosophers such as Moritz Schlick or Hans Reichenbach. That may be one of the reasons why they were so enthusiastic about relativity. There is a conjecture that Einstein's argument may have, as one of its possible sources, Joseph Petzoldt, a positivist philosopher (as well as Erich Kretschmann's article; see Howard & Norton 1993, 51-2).
However, there may well be a "deeper" reason than "positivistic" reason, for Einstin's thinking. John Stachel warns that we should not attribute trivial or mathematically naive errors to Einstein (and Grossmann), when he convinced himself of the correctness of the original "hole" argument. What is at issue is the question of physical identity or physical difference between G(x) and G'(x) (or between gmn and g'mn) in the same coordinate system K. According to Stachel, the question depends on how we individuate (physically) a point or a process, according to the physical theory in question. Notice that the metric tensor g'mn (within the hole) of the second solution was "dragged along" from the solution in K'. Thus if there is no way to individuate a point within the hole (the red spot, e.g.), other than by means of this field (expressed either by gmn or by g'mn), we cannnot individuate two distinct points, even if we have two mathematically distinct solutions in the given coordinate system K. The answer is quite different, if we have other independent criterion for individuation; e.g., if we may assume an absolute space as a physical entity, then we can individuate two points, not relying on geodesics or gravitational fields, but this is not the case with Einstein's general relativity, where there are no nondynamical processes. Thus, in short, Einstein's point of "point coincidence" argument is that we have no other way to individuate two physical events or two geodesics, etc., than by those properties determined by the (generally covariant) field equations---this is Stachel's interpretation (1989, 74-80, 84-88). Thus we should be careful, not to ascribe directly a positivist philosophy to Einstein for his way out.
References
Earman, J., Janssen, M., and Norton, J.D., eds., (1993) The Attraction of Gravitation, Einstein Studies vol. 5, Birkhaeuser.
Howard, D. and Stachel, J., eds. (1989) Einstein and the History of General Relativity, Einstein Studies vol. 1, Birkhaeser.
Howard, D., and Norton, J.D. (1993) "Out of the Labyrinth? Einstein, Hertz, and the Goettingen Answer to the Hole Argument", in Earman et al 1993, pp. 30-62.
Stachel, J. (1989) "Einstein's Search for General Covariance, 1912-1915", in Howard &Stachel 1989, pp. 63-100.
For an excellent review article by John D. Norton on the Hole Argument, see Stanford Encyclopedia of Philosophy, http://plato.stanford.edu/entries/spacetime-holearg/
August 30, 2000; last modified March 28, 2003. (c) Soshichi Uchii