

Goedel's Universe
Japanese version, pdf. (revised 1 Jan. 2007)
Published version: 『現代思想』35-3、186-195、2007年2月。
This year, 2006, is the 100th anniversary of Kurt Goedel's birth. Although he was primarily a logician, unlike many other logicians, he published a couple of papers on general relativity. And in this field, he is known for the Goedel Universe, a cosmological solution of Einstein's equation of gravitational field (with the cosmological constant; in Goedel's solution, its value becomes negative). What is it like? Here are some illustrations (I owe a great deal to Hawking & Ellis 1973 and Malament 1985).
The Goedel universe is a homogeneous and stationary universe, but it has a rotation; this rotation may seem innocuous at first sight, but it produces peculiar features quite unlike other cosmological models known before Goedel's 1949 paper. Here is a diagram for the Goedel universe.
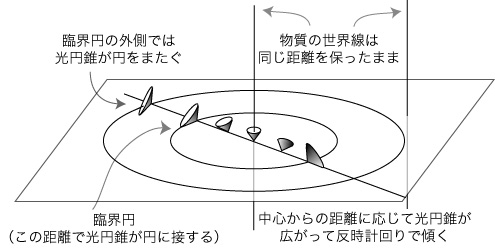
Figure 1. Light-Cones in the Goedel Universe
Two vertical lines are a world line of a matter particle (which may be regarded as a galaxy). These particles are always at the same distant. However, the center vertical line is a center of rotational symmetry. Any matter particle (which is a free-float system, a local Lorentzian system) can be regarded as such a center. The whole universe is rotating just as a rigid body rotates; you can see the point by the following Figure 2. The angular velocity can be measured by referring to a gyroscope (which indicates the same direction) at any matter particle; and, as (1) and (2) in the Figure show, the angular velocity is the same at any two points.
Figure 2. Rotation of a Rigid Body
Now, this rotation (which Goedel introduced into his model) produces a peculiar effect on the light-cones, as is shown in the Figure 1. The center light-cone is up-right, but as we go farther from the center, the light-cone tilts and widens. For, the universe is rotating around this center (and by symmetry, around any matter particle), and according to special relativity, the velocity of a particle changes the hypersurface of simultaneity and also the direction of the time axis.
This point may be understood easily, by simplifying the matter in terms of special relativity. For it is a simple application of the relativity of simultaneity. If you move (uniformly) relative to someone, your time axis and your space (hypersurface of simultaneity) tilt, as in the following figure (t-x at rest, and t'-x' moving frame).
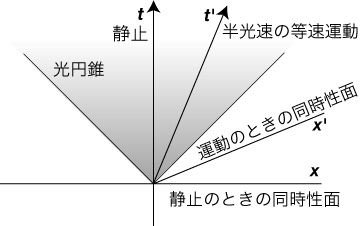
Figure 3. The Relativity of Simultaneity
And if the universe rotates, relative to a local Lorentian frame, the tangential velocity increases as one goes farther from the center of rotation; and the relativity of simultaneity comes in. Suppose A is the center and B is a location at some distance from A. Then the time axis and the space (hypersurface of simultaneity) at B tilt. In addition, the rotation produces a gravitational field (the velocity of light changes and a light ray curves). The effect is that the light-cone there (its time axis must be orthogonal to the space there) tilts, relative to the original space at A.
In the Goedel universe, there is a critical distance from the center; at this distance, the light-cone becomes tangent to the plane (hypersurface) of simultaneity of the central light-cone. And beond this critical circle, the light-cone straddle the plane. This means that a light ray can go below the plane.
This makes a time-travel possible! I mean, a time-travel to your past! Here is the second figure (light-cones are not necessarily correctly depicted, for the sake of graphical representation; in the Goedel universe, all matter world lines must be timelike, i.e. within the light-cone at each point) which illustrates this time-travel.

Figure 4. The Time-travel to your past!
Imagine that your galaxy was once at p of the Figure 4. Now you are at q. In order to visit p again, (1) you first accelerate and aim at the outside of the critical circle. Then, (2) when you passed the critical circle, you go downward for a while, enough below the original hypersurface at p. Next, (3) you aim at the critical circle (below p, of course), and if you passed it, you aim at p, from the past region of p. Thus you came back to your past, by going, everywhere, to your future! This makes defining the cosmological time (common to all particles of matter) impossible.
References
Goedel, K. (1949) "An example of a new type of cosmological solutions of Einstein's field equations of gravitation", Review of Modern Physics 21 (1949), 447-450; Kurt Goedel Collected Works 2, 190-198.
Goedel, K. (1949a) "A Remark about the Relationship between Relativity theory and Idealistic Philosophy", in Albert Einstein, Philosopher-Scientist (ed. by P. A. Schilpp), 557-562; Kurt Goedel Collected Works 2, 202-207.
Hawking, S. W. and Ellis, G. F. R. (1973) The Large Scale Structure of Space-Time, Cambridge University Press.
Malament, D. (1985) "'Time Travel' in the Goedel Universe", PSA 1984 (ed. by P. Asquith and P. Kitcher), vol. 2, 91-100.
Last modified March 2, 2007. (c) Soshichi Uchii
webmaster