|
ÈwNwj [Y^[ |
![]()
No. 58, June 21, 2005
Book Review by Soshichi Uchii:
Brian Greene, The Fabric of the Cosmos, Allen Lane (Penguin), 2004. Lee Smolin, Three Roads to Quantum Gravity, Basic Books, 2001. |
 |
These are two of the most exciting books I have read this year. On the one hand, as you may already know, Brian Greene is the author of The Elegant Universe (1999), which became one of the world's best sellers, comparable to Hawking's Brief History of Time. His second book is as good as the first one, and this time he explores the nature of space and time on the basis of the superstring theory. On the other hand, Lee Smolin is one of the most active advocates of the loop quantum gravity, which aims at a consistent quantum theory of gravity; it has been a big problem to be solved that we should construct a theory of gravity applicable on a very small scale (at the quantum level), since general relativity, though quite successful on a larger scale, has long resisted to be quantized (i.e. theorized in terms of discrete quantum, not in terms of continuous mathematics). Smolin's main theme is also space and time. Thus I wish to review the two books at the same time.
Differences between the Two Approaches
These two authors are quite successful in telling their stories of space and time, touching on many other topics relevant to their main subject. But the general reader may wonder at the outset: what on earth aregsuperstring theoryhandgloop quantum gravity"? All right, let's briefly prepare for this question. Brian Green writes as follows:
String theory and loop quantum gravity both claim to have achieved the long-sought goal of providing a quantum theory of gravity, but they do so in very different ways. String theory grew out of the successful particle physics tradition that has for decades sought matter's elementary ingredients; to most early string researchers, gravity was a distant, secondary concern, at best. By contrast, loop quantum gravity grew out of a tradition tightly grounded in the general theory of relativity; to most practitioners of this approach, gravity has always been the main focus. A one-sentence comparison would hold that string theorists start with the small (quantum theory) and move to embrace the large (gravity), while adherents of loop quantum gravity start with the large (gravity) and move to embrace the small (quantum theory). (Greene 2004, 489)
To add a few supplementary remarks, according to the string theory, the things in the world are supposed to be consisting of a number of tiny strings whose various vibrations produce what are usually calledgparticleshsuch as electrons, protons, and many others. This assumption of tiny strings (small but finite) is conducive for eliminating theginfinitieshwhich tend to appear if we try to combine general relativity and quantum mechanics for treating the phenomena on a small scale. On the other hand, loop quantum gravity is so-called because small loops appear as essential ingredients of geometry, when we wish to describe gravity on a small scale. What is exciting about these loops is thatgtheir interrelations defined spaceh(Smolin 2001, 128). That is, we don't have to presuppose (like Newton) space and time in order to investigate gravity at the quantum level, but we can construct space out of loops (N.B. not points).
This is the feature of loop quantum gravity that is called background independence. As Smolin puts it:
Time is described only in terms of change in the network of rlationships that describes space. This means that it is absurd in general relativity to speak of a universe in which nothing happens. Time is nothing but a measure of change---it has no other meaning. Neither space nor time has any existence outside the system of evolving relationships that comprises the universe. Physicists refer to this feature of general relativity as background independence. By this we mean that there is no fixed background, or stage, that remains fixed for all time. In contrast, a theory such as Newtonian mechanics or electromagnetism is background dependent because it assumes that there exists a fixed, unchanging background that provides the ultimate answer to all questions about where and when. (Smolin 2001, 24-5)
And here appears the crucial difference between string theory and loop quantum gravity. According to Greene,
the main failing of current formulations of string theory is that they presuppose a background spacetime within which strings move and vibrate. By contrast, the main achievement of loop quantum gravity---an impressive one---is that it does not assume a background spacetime. Loop quantum gravity is a background-independent framework. (Greene 2004, 490)
Moreover, the background spacetime string theory presupposes is no ordinary spacetime; it has 10 dimensions or 11 dimensions (for the as yet emerging M theory, which is supposed to unify all different versions of string theory). This makes a number of people suspicious of string theory; isn't its assumption too strong?
But, of course, a strong side has the other, the weaker side, and this applies to both theories. Recall the classic example of Newton vs. Leibniz. As a scientific theory, the Newtonian mechanics is by far the greater, since it achieved a great synthesis and a great empirical success in various field; Leibnizian mechanics based on the relational concept of space and time could not even take off (Mach and Poincare later suggested an improvement, but its realization came only in the late 20th century, around the 90s). However, as regards the philosophical basis, Leibniz seems to be superior, since he can dispense with external and absolute space and time; Leibniz's vision of science (physical science) seems to be far more attractive than Newton's, since it can dispense with ad hoc divine interventions.
However, despite the crucial difference between string theory and loop quantum gravity, the picture of space and time which emerges from the two theories share a basic common feature: it has a discrete structure (Smolin callsgatomic structure"), which becomes significant around the Planck length (if we consider one dimension), which is 1 cm divided by the 33rd power of 10!.
Greene on Newton's Bucket
So much for the general remarks, and let us see some of the highlights of these two books. Greene's book has five parts, and of course the author intends something by this division. But I will ignore this altogether, and concentrate on what seem most interesting to me, or to the general reader. From this perspective, I will first recommend to go through chapter 2 and chapter 3, where the main theme is the famous Newton's bucket. This was already discussed by various people, but its lesson is not clearly recognized by most people outside the narrow circle of the philosophers of space and time. Thus Greene's first contribution is that he has made its lesson quite accessible to the general reader.
Here is a figure (by myself) which illustrates the point of Newton's argument. He wants to show that mere relative motions are not sufficient for explaining the result of this experiment, and argues for the need for absolute space.
FIGURE 1. Newton's Bucket
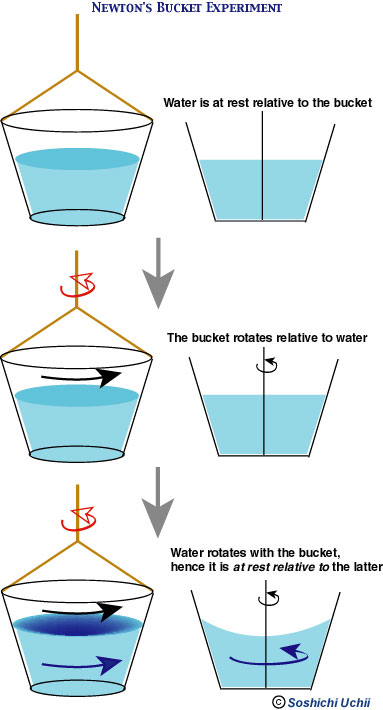
An external force is applied to the bucket, and this generates the rotation of the bucket; but initially only the bucket rotates. But then the rotation is transmitted to the water, and the water rotates with the bucket, with the same angular speed; but notice that the two are at rest to each other. However, there appears a conspicuous difference, due to the rotation of the water. This proves, Newton says, that no relative motion can explain this phenomenon; only absolute motion can.
Leibniz's objection against absolute space and time were long ignored until the late 19th century, when Ernst Mach began assault on the Newtonian mechanics. Mach in effect said that Newton was too quick to invoke absolute space for explaining the bucket experiment. Although the bucket and the water may be at rest to each other, there are many other things around the bucket, the fixed stars, in particular. We can tell the bucket and the water are spinning relative to them; if absolutely nothing existed around the bucket, how can we tell it is spinning? Thus a new question emerges. As Greene puts it:
Imagine now that you are immersed in the blackness of completely empty space: no stars, no galaxies, no planets, no air, nothing but total blackness, c This time, if you start spinning, will you feel it? c In this example c there is absolutely no way for you to distinguishgnot spinninghfromgspinning" by comparisons with other material objects; there aren't any other material objects. c Mach argued that in an otherwise empty universe there is no distinction between spinning and not spinning---there is no conception of motion or acceleration if there are no benchmarks for comparison c (Greene 2004, 34)
But how can we decide which is right, Newton or Mach? Greene now goes through special relativity and general relativity, and clarifies the answers given by these theories (which Mach did not know).
(1) According to special relativity, even in an otherwise completely empty universe, the bucket's spinning makes sense (it is spinning with respect to absolute spacetime) and the surface of the water becomes concave. (See Greene 2004, 51, 58-61.)
(2) According to general relativity, spacetime is not absolute anymore as was the case in special relativity; spacetime evolves together with matter, according to the Einstein equations. However, on our setting of the question, the universe is completely empty except for the bucket and the water in it. Although the benchmarks for all motion are freely falling observers (in the gravitational field), not absolute spacetime, the question reduces to the case of special relativity, since there is no gravitational field (or, in other words, there is a flat gravitational field) in an empty universe. Thus the water becomes concave again, even according to general relativity! (See Greene 2004, 72-4.)
Thus, in spite of Mach's criticism, Newton was right after all! However, this is not the end of the matter.
Frame Dragging
Actually, Mach made another important suggestion when he criticized Newton's bucket experiment. He saidgno one is competent to say how the experiment would turn out if the sides of the bucket increased in thickness and mass till they were ultimately several leagues thick". Einstein was certainly influenced by this idea, and he began the following sort of thought experiment: Suppose a test particle is placed at the center of a spherical shell; what is going to happen if the shell begins an accelerated motion? A certain force acts on the particle, and it isgdragged", in a sense.
FIGURE 2. Einstein's Shell
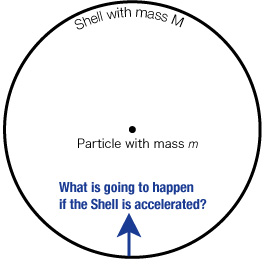
Einstein's tentative calculation (1912) suggested such an effect which may be pleasing to Mach. Later, this effect is known by the name ofgLense-Thirring effect", or frame-dragging in general. That is, a massive object, if it spins, drags space around it; in particular, if a massive shell spins around a bucket with water, the space within the shell is dragged, and hence the water is dragged, so that its surface becomes concave! Greene gives a popular exposition of this effect (Greene 2004, 416-8), the calculation of which was finally completed in 1985 by Herbert Pfister and K. Braun. Right now the projectgGravity Probe Bhis going on as a joint project of Stanford and NASA; and its objective is to measure the frame dragging around the earth by using precise instruments launched on a satellite (April 2004; results are still to be expected, because of a series of troubles).
The Direction of Time
Another topic Greene pursues in depth is the direction of time, how to explain the difference between past and future. Eggs fall, cracking and splattering, but we never see splattered eggs and eggshells gather together and coalesce into uncracked eggs (Greene 2004, 143). Why is that, and how can we explain that by the laws of physics? This problem is far harder than you may imagine. Eminent scientists and philosophers, such as Boltzmann and Reichenbach, tried to explain this in terms of the laws of physics but they failed. For, the fundamental laws of physics are symmetric with respect to time-reversal. Thus although Boltzmann argued that we may distinguish future from past in terms of a far higher probability of increasing disorder (another name is entropy), the same argument applies to the past as well: given the present condition, the probability of disorder increases even toward the past. For Boltzmann's statistical mechanics, the basic law is Newtonian mechanics (time-reversal symmetric), and even if we add probabilistic consideration on a vast number of molecules and their configurations, the problem cannot be solved (probabilistic laws are also time-reversal symmetric). Green now tries, drawing on Roger Penrose's idea that the cosmological considerations may supply the key. In a nutshell, the current order is a cosmological relic (Greene 2004, 171), and the ultimate source of order, of low entropy, must be the big bang itself (173). Greene tries to work out the detail of this scenario. The key point is the connection between disorder (entropy or high probability) and gravity. I will recommend to go through Greene's argument (170-6, and 213-16 for quantum mechanical twists; further cosmological twists come on 313-23).
However, there still remains a crucial question. Even though the inflationary cosmology suggests repeated occurrence of inflation (each occurrence producing a universe; so that the universe like ours emerges not as a miracle but with a substantial probability), we know next to nothing about the pre-inflationary realm. Thus we need a new theory which can give an answer, or even an approximation, to that question. Greene naturally recommends superstring theory. What sort of picture of space and time can it provide?
M-Theory and the Brane World Scenario
To make a long story short, let's start from the so-called M-theory, the promising candidate for unifying all different versions of string theory. It assumes an 11-dimensionnal spacetime (10 for space, 1 for time). Tiny strings, either closed (loop) or open, are supposed to move and vibrate in this background. These strings are extremely tiny but finite in length, and that is the prerequisite for unifying quantum mechanics and general relativity, since for point-like particles infinity easily appears and that destroys physics! Seems reasonable, but why can't we see more than 3 spatial dimensions? The answer is that additional dimensions are curled up (on a very small scale) in a complicated figure, so that not only in everyday life but even in precise high-tech experiments we cannot detect them (so far).
There is another assumption, called supersymmetry, hence the name "superstring theory". Elementary particles have a property called "spin", but its value may be either an integer (1 or 2) or a half-integer (1/2, e.g.). Supersymmetry demands that each vibrational pattern (corresponding to a particle) has another which differs by 1/2 in spin. This multiplies the number of vibrational patterns (hence the number of particles), but string theorists believe the theory becomes better this way.
Originally, string theorists claimed strings (1-dimensional, of course) are basic, but the situation has changed because of M-theory; it allows higher dimensional ingredients called membrane, e.g. 2 dimensional 2-brane, 3-brane, etc. And this opened a new prospect: we may be living in a 3-brane! Of course, this is still a very speculative attempt, but a growing number of people are now pursuing a cosmology in terms of branes. In a nutshell, there may be more than one brane world, and the endpoints of an open string may be stuck to a brane or branes! In particular, photons are open strings with endpoints trapped in a brane, so that they (hence light) cannot leave that brane; this means the electromagnetic force (its field is composed of photons) is confined to the brane. The same is true of the weak force and the strong force. The only exception is graviton, the messenger of gravitational force. Gravitons appear as a vibrational pattern of closed strings (no endpoints), and it can reach extra dimensions! Utilizing this special feature, Steinhardt and Turok proposed a new framework for cosmology.
Suppose our universe is contained in a 3-brane, but there is another 3-brane in our vicinity. If the two collide, then similar conditions to a big bang and inflation appear, leading to expansion and cooling, then forming galaxies etc. Now, for the standard inflationary cosmology, the source of a large portion of energy in our universe was a riddle, calledgdark matter" orgdark energy", but the brane world scenario can supply the source: the gravity from the other brane! In addition, it can explain the newly discovered inflation of our universe: about 7 billion years ago, the expansion of our universe began to accelerate again (this was an observational discovery in 1998)! To accommodate these two riddles, Steinhardt and Turok propose a cyclic model, going through collision, expansion, attraction of the two branes, collision again, etc., but we will skip the details.
Although the brane world scenario is indeed interesting, for the reader who expected an improved answer to the problem of the arrow of time, or for the reader who wished to clarify the notion of space and time, this scenario seems disappointing. For, this scenario introduced stronger assumptions. To put it bluntly, 11-dimensional spacetime was simply assumed, and a 3-brane in it is said to be our 3-dimensional space. Are you satisfied with this? But despite this complaint, we should thank Greene's readable exposition of the newest brand of cosmology.
Smolin's Philosophical Stance
Let us now turn to Smolin's book. His book begins with several philosophical assertions. (1) There is nothing outside the universe (Smolin 2001, 17); in particular, observers are within the universe. (2) The logic for the working cosmologist is not classical (statements are either true or false), but intuitionistic or topos theory (refined version), which allows us to say gwe can't tell now whether it's true, but we might be able to in the future" (Smolin 2001, 30). (3) As regards the interpretation of quantum theory, the slogan should be: Many observers, not many worlds (Smolin 2001, 48). (4) The universe is made of processes, not things. Relativity and quantum theory, according to Smolin, tells us that our world is a history of processes (motions and changes), a smallest unit of it being an event (Smolin 2001, 53). Thus the universe is relational (relations of events) and continually evolving.
Smolin makes these four his points of departure. What are then the three roads to quantum gravity? The first is string theory, and the second is loop quantum gravity, as we have already seen at the beginning of this review. The third consists of several independent attempts that look for a new framework. Since we have already reviewed Greene's book, let us see new features that are not already covered.
Black Holes and Their Entropies
The first surprise comes from close studies of black holes (chh. 5-8). Today, many people already know that a black hole has a hidden region; no one can see, from outside, the inside of the horizon of a black hole, since nothing (including light) can escape from it. But we can approach the horizon, and even stay just above it, if our spaceship has powerful enough engines; but for this, engines must continually work, accelerating the spaceship so that it can stay outside of the horizon. But what is going to happen, if you accelerate? Here we have to take both relativity and quantum mechanics into consideration.
To make things easier, forget about the black hole for a while, and imagine the spaceship accelerates in an empty space. For this case, Smolin quotes Bill Unruh's law: Accelerating observers see themselves as embedded in a gas of hot photons at a temperature proportional to their acceleration (Smolin 2001, 86). Remember the spaceship is supposed to be in an otherwise empty space, no stars, no black holes around it! Then where do those photons come from? According to quantum mechanics, and according to Heisenberg's uncertainty principle in particular, no particle can sit still; it suffers what Greene calledgquantum jitter". And this applies to fields too; there remain quantum fluctuations of the vacuum (where electromagnetic fields can exist). And what is surprising is that these fluctuations can be detected by accelerated observers. Acceleration means that energy is continually supplied, and this energy can be transformed into photons.
But what is heat? It's the mean kinetic energy of randomly moving particles; hence the photons detected by accelerating observers have a temperature above the absolute zero. Another source of randomness is the notorious non-local correlation (a clear example is EPR paradox) that is essential in quantum mechanics, unlike other physical theories such as general relativity. Photons in the gas surrounding the accelerating spaceship are correlated with photons in other regions hidden to the spaceship. Yes, acceleration generates a hidden region; light signals from there cannot reach the spaceship (Smolin 2001, 79; also see Uchii 2004, 66 and 79). "Hidden" means the information does not reach, andgheat" is closely connected with the notion of entropy; thus emerges the relationship between information and entropy (but I will not get into any depth in this review). This relation is summarized in Bekenstein's law: With every boundary separating observers from a region which is hidden from them, there is associated an entropy which measures the amount of information which is hidden behind it; this entropy is always proportional to the area of the horizon (Smolin 2001, 86-7).
Although the hidden region for the accelerated spaceship disappears if the acceleration disappears, and hence the case is somewhat different from the case of a black hole, Unruh's and Bekenstein's laws apply equally to black holes. That is, a black hole can have a temperature (above the absolute zero), and it can also have an entropy, a measure of information hidden within the horizon.
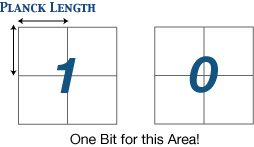
As you may well know, the amount of information can be measured in bits, which can be interpreted as the number of yes/no questions whose answer can be coded in signals. But isn't the information hidden in a black hole infinite, since its volume may contain infinite number of spacial points? The answer is, again surprisingly, No. Look again Bekenstein's law; entropy or (missing) information is related with the area of horizon, not the volume. Further, this relation has a simple and definite quantitative form. If we measure the area in terms of Planck length, a unit area is the square of Planck length. Then the entropy is simply one quarter of the area, measured in this unit. In other words, one bit for every four square cells whose edge has Planck length (Smolin 2001, 103). This strongly suggests that spacetime also may have discrete structure (Smolin often calls "atomic structure"), at the level of Planck length.
FIGURE 3. Planck Units

FIGURE 4. Bit for 4 Planck Areas
Moreover, Bekenstein's law sets the limit, Bekenstein's bound. Since a black hole is a limit of a certain amount of mass concentrated in one region, its surface (horizon) determines the upper limit of entropy (missing information) for that area. This is the bound to the information which can be contained in that region of space.
The Road to Loop Quantum Gravity
Now comes the major part of Smolin's book. He tells us a quite illuminating story: how he and his colleagues succeeded in constructing a viable theory of quantum gravity (chh. 9 and 10). The constituent ideas for loop quantum gravity have several different sources. First comes the idea of quantized field lines; for example, the magnetic field of superconductor splits into discrete (quantized) flux lines (Smolin 2001, 109). Then Ken Wilson's discrete lattice, on which such quantized flux can be represented, as a string between two nodes. This can apply not only to electricity and magnetism but also to quarks. And this is the source of the wordgloop" (although Smolin does not give us a complete explanation why loops appear out of strings). A. Polyakov was also working on a similar idea, but without lattice structure. Why not, then, apply a similar idea to gravity? This was Smolin's twist, and he worked out his first paper. But soon he realized this paper was a failure, because, as was told by the mature Smolin in his book,gWilson's lattice was an absolute, fixed structure and thus clashed with the relational nature of Einstein's theory of gravity" (Smolin 2001, 119), andgthe lattice itself would have to become a dynamical structure which could evolve in time" (ibid.).
This recognition was reinforced by his acquaintance with Julian Barbour (who was relatively unknown then, but a powerful advocate of Machianism and relationalism). But Smolin acknowledges that the turning point was the revival of string theory (Smolin 2001, 122). And he worked in this field for a while, in order to look for a background-independent theory which would reduce to string theory as an approximation. And in this period he encountered Ashtekar-Sen formalism for general relativity; Einstein's field equations were simplified, and changed into a form more friendly to quantum chromodynamics (dynamics for quarks). Eventually, this brought about a breakthrough.gOne day in February 1986, Ted [Jacobson] and I, working in Santa Barbara, set out to find approximate solutions to the equations of quantum cosmology, c All of a sudden we realized that our second or third guess, which we had written on the blackboard in front of us, solved the equations exactly" (Smolin 2001, 40). The equations referred to here are calledgWheeler-DeWitt equations" (which appeared in the 60s); roughly, they are quantum (Schroedinger) equations for the whole universe (don't say this is nonsense, for we are now pretty safe for saying that our universe was very small when it was born!). They tell us which state of the universe may be realized with such-and-such probability.
However, there still remained a few problems including a hard one: they had to prove that their solutions are indeed background independent. And its solution came from a physicist belonging to the third road: Carlo Rovelli, who was a student of Chris Isham (an Oxford theorist who belongs to the third road), gave it (Smolin 2001, 129-30). Thus it became possible to complete the picture that, on the Planck scale, loops interact with each other, and their dynamic evolution determines the structure of space and time. This is loop quantum gravity. For the specific manner of the evolution, which can be expressed in terms of "spin networks" (Roger Pensose's invention), the latter half of chapter 10 is devoted.
The Holographic Principle
Although Smolin gives a brief exposition of string theory, we will skip it, and proceed to chapter 12 where "holographic principle" is discussed. Black hole thermodynamics, loop quantum gravity, and string theory all indicate that space and time must be discrete when viewed on the Planck scale. But each approach may be indicating different aspects of the world, and if so, we may expect there emerges a unifying principle which can combine different approaches into one. Smolin takes up the holographic principle (also discussed by Greene) as a possible candidate for such unification.
A hologram is a two-dimensional plate, which, when illuminated by laser light, produces a three-dimensional image. But what does this have to do with quantum gravity? Recall Bekenstein bound which sets a limit on the amount of information contained in a region of three-dimensional space. What is surprising about this is that the bound is proportional to the two-dimensional area, not to the three-dimensional volume. Thus, to speak figuratively, if we want to construct the most efficient memory device out of the quantum geometry of space, it should be a two-dimensional surface, and one bit can be saved on every four Planck areas. Thus, to put it bluntly, suppose the Thing we want to know is covered by the Screen through which all information flows; then one may assert that if we want to know the Thing, all we need is the information on the Screen. Then, isn't the Screen just sufficient for representing the Thing, or more radically, isn't there any difference between the Screen and the Thing? This suggests the strong holographic principle: the system on the Screen may be regarded as the Thing itself, since there is no way to tell the difference for the observer.
Smolin, however, reformulates the principle as follows. He asserted, at the outset, that the universe is made of processes, not things. Thus what he recommends is the weak holographic principle which states thatgwe are mistaken to think that the world consists of Things that occupy regions of space. Instead, all that there exists in the world are Screens, on which the world is representedh(Smolin 2001, 177). The point is that there is only one kind of entity,grepresentations by which one set of events in the history of the universe receives information about other parts of the world" (ibid.). Moreover, we have to recall that Smolin said, also at the outset,gmany observers, not many worlds". Incorporating this idea, Smolin now asserts:
Thus, it is not enough to say that the world is a hologram. The world must be a network of holograms, each of which contains coded within it information about the relationships between the others. In short, the holographic principle is the ultimate realization of the notion that the world is a network of relationships. (Smolin 2001, 178)
This picture strongly reminds us of Leibniz's monadology, each monad representing the rest of the world!
In conclusion, then, I will most warmly recommend these two books by Greene and Smolin, each written from a different perspective; each contains a systematic and up-to-date survey of recent developments; and their exposition is clear and exciting. Both books are compulsory readings for anyone interested in the philosophy of space and time.
References
Barbour, J. and Pfister, H., eds. Mach's Principle (Einstein Studies
6), Birkhaeuser, 1995.
Einstein, A. gGibt es eine Gravitationswirkung, die der elektorodynamishen Induktionswirkung analog ist?", Vierteljahrschrift fuer gerichtliche Medizin und oeffentliches Sanitaetswesen 44, 1912.
Greene, B. The Elegant Universe, Vintage Books, 1999.
Uchii, S. Tracing Einstein's Ideas [in Japanese], Minerva, 2004.
Last modified Dec. 1, 2008.(c) Soshichi Uchii
