|
科学哲学ニューズレター |
![]()
No. 42, July 10, 2001
Book Review by Soshichi Uchii:
The End of Time, or the Beginning of the New Machianism?
The End of Time by Julian Barbour
Editor: Soshichi Uchii
The end of time, or the beginning of the new Machianism?
Are Leibniz and Mach refuted?
As we can see in Leibniz-Clarke Corrspondence, Leibniz did not succeed in refuting the Newtonian theory of absolute space and time. On the contrary, he had a grave difficulty for explaining Newton's experiment on the bucket (acceleration produced by rotation), for explaining the quantity of space and time, and for reconciling his admission of true and absolute motion with the relational theory. Further, Euler later pointed out the crucial difficulty of the relational theory: the laws of motion (the law of inertia, in particular) do not seem to be reproducible in terms of the relational theory.
Although it is well known that Ernst Mach criticized Newton, and tried to reconstruct mechanics only in terms of relative motions, this remained only a crude idea. Further, it is also well known that Einstein said that, inspired by Mach's criticism of Newton, he tried to incorporate Mach's idea into the general theory of relativity; but it is now generally acknowledged that the general relativity is not a relational theory (as some philosophers of science thought on the heyday of the logical positivism). Some even argue that the theories of relativity are more unfriendly, than the classical mechanics, to the relational idea.
Is it then the case that, since nearly 300 years passed without any viable candidates of mechanics or dynamics on the basis of the relational idea, we have to conclude the relationism is over? No, to conclude so would be premature, since the modern attempts at relational theories of dynamics have the history of only 25 years or so. This may be surprising to many, but the situation may become less surprising if you understand that most physicists cannot afford to spend much energy on such philosophical works as this. For, what is the merit even if you succeed in reconstructing the Newtonian mechanics on the relational basis? You cannot obtain any academic position by such a work, let alone the Nobel Prize!
Thus the physicist Julian Barbour recalls in the Preface of his new book The End of Time, the circumstances in the late 1960s:
But even then there was pressure to 'publish or perish'. If you could not turn out one or two research papers each year (now, crazily, one is expected to produce four or five) and do all the teaching and administrative duties, I was warned, you could not look forward to much of a career. But I might want to spend years thinking about basic issues before publishing anything. (Barbour 2000, 3-4)So Barbour chose his own, unconventional way. He decided to earn money by translating Russian scientific journals, and to do physics at his leisure.
I greatly valued the feeling that I could do just what I wanted when I wanted. ... I had the luxury of being able to work on topics other physicists felt they could not risk, either because nothing might come of the work or because their reputations would suffer. (Barbour 2000, 4)But what did Barbour want to work on? He wanted to pursue foundational questions: What is time? What is the most fundamental in physics, spacetime, or what else? Is Newton's way in terms of absolute space and time correct? What about relativity? And how do we unite relativity with quantum mechanics? By pursuing these questions, he became one of the leading Machians of the day.
... while thinking hard about time, I came across Mach's book. Like so many others, I was captivated by his idea about inertia. His comments on time also encouraged me greatly: 'It is utterly beyond our power', he said, 'to measure the changes of things by time. Quite the contrary, time is an abstraction, at which we arrive by means of the changes of things.' this was just the conclusion I had reached. A year or so later, after I had decided to study the foundations of physics, I started to read the papers Einstein had written when he was creating general relativity. Comparing them with what Mach had written, I came to the conclusion that Einstein had simply not set about the problem in the right way: he had not attacked it directly. It seemed to me necessary to go back to first principles. (Barbour 2000, 67-68)
Platonia or the Relative Configuration Space
What does Barbour mean by this? Recall Einstein already had the special relativity and the Minkowski space, a substitute for Newton's absolute space and time, when he embarked on the general relativity. Barbour, in contrast, needed "a new arena in which to describe the universe" (Barbour 2000, 68); that is the relative configuration space of the universe, or what he calls "Platonia".
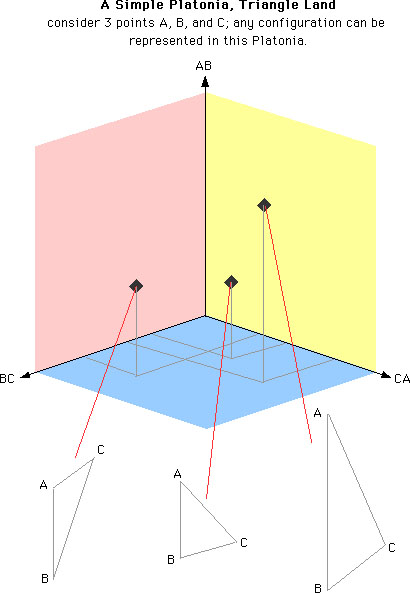
What is the reality of the universe? It is that in any instant the objects in it have some relative arrangement. If just three objects exist, they form a triangle. In one instant the universe forms one triangle, in a different instant another. What is to be gained by supposing that either triangle is placed in invisible space? The proper way to think about motion is that the universe as a whole moves from one 'place' to another 'place', where 'place' means a relative arrangement, or configuration, of the complete universe. (Barbour 2000, 68-69)Here, one can recognize a strong analogy with Leibniz's idea that "space is a collection of all places" defined in terms of relations among them (see Leibniz-Clarke correspondence, pt. 2). But Barbour's idea has an additional virtue, since "time" also can be incorporated; according to him, each configuration (a point in Platonia) can be regarded as a possible "Now", a possible time-instant. Actually, although there are time-instants in Platonia, Platonia is a timeless arena, as we will see shortly. Mach may not have denied the existence of time, but he said, "It is utterly beyond our power to measure the changes of things by time. Quite the contrary, time is an abstraction, at which we arrive by means of the changes of things". So Barbour regards changes more basic than time, and as a consequence, he came to the view that time does not exist. But, now, let me insert a figure for illustration (adapted from Barbour's Figure 3; the three axes represent the length of each side of a triangle, respectively).
The 2-snapshots Problem
Suppose, then, the three particles A, B, and C (each apex of a triangle in the Figure) interact with each other, and change their relative positions; what is the law governing such changes, and given certain information, how can we predict a change? These are questions of mechanics or dynamics. The answer to these questions according to the Newtonian mechanics should be well known. We have three laws of motion and the law of universal graviation; so that, given the three masses, their initial positions and their initial velocities (including directions), their history is uniquely determined (Laplace's demon). However, the concepts of position and velocity presuppose the absolute space and time; so if you stick to the Machian idea, this may not be acceptable. Further, we have to notice that there is no time-axis in Platonia.
However, we can see that a "history" of the three particles (according to the law) can be, in a way, represented by a single curve (red, in the following Figure) in the Platonia (Triangle Land), as in the following Figure.
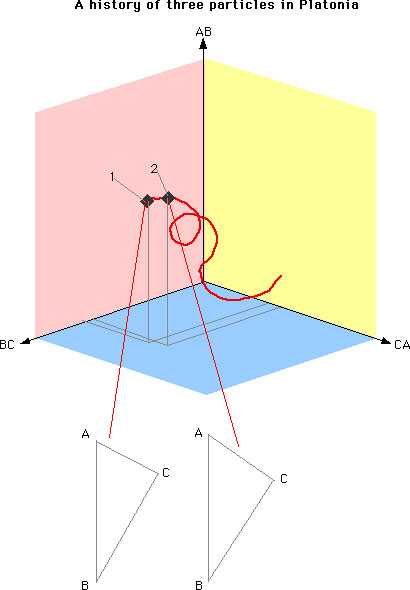
In our Platonia, we do not have information of "positions" nor of "velocities" of the three particles A, B, and C, since each point in Platonia represents a configuration of the three particles. So, taking the Machian stance (i.e., sticking to the relational idea), Barbour now asks: what is needed in order to determine a path (curve according to the law) in Platonia? If we can obtain a reasonable answer to this question, and can specify the appropriate law connecting any two points on such a path (say, the point 1 and the point 2 in the Figure), we have a Machian dynamics; moreover, we may be able to reconstruct the Newtonian mechanics in terms of the relational idea. But this is only a first step. Is similar reconstruction possible for general relativity? And what about quantum mechanics? Barbour indeed treats these questions later, but for now let us concentrate on the Newtonian mechanics.
If Mach is right, so that time is nothing but change and all that really counts in the world is relative distances, there should be a perfect analogue of Laplace's scenario with a divine intelligence that contemplates Platonia. Machian dynamics in Platonia must be about the determination of paths in that timeless landscape. It should be possible to specify an initial point in Platonia and a direction at that point, and that should be sufficient to determine the entire path. (Barbour 2000, 76)As an approximation, imagine two triangles (represented by point 1 and point 2 in the Figure) slightly different from each other; this pair would give an "initial point" and a "direction at that point" (it does not matter which is taken as the initial point, but we take point 1 in the Figure). Given appropriate qualifications (including the "time separation" in the Newtonian frame--which amounts to the relative time--between the two points), are these two triangles sufficient for determining a path? Barbour credits Poincare for putting the question in this form and giving an answer:
He [Poincare] concluded regretfully that a mechanics that uses only relative quantities, as Mach advocated, cannot get off the ground. It lacks perfect Laplacian determinism. Nevertheless, the failure is curious. Absolute space and time could have had an effect through all the freedoms allowed in the placing of the two triangles. There are fourteen degrees of freedom in total, of which ten have no effect whatsoever. This is just what the invisibility of space and time would lead us to expect. Yet four degrees of freedom do have a profound influence. Three are associated with twists in space, the fourth with the overall speed put into the system. (Barbour 2000, 83)Thus with points 1 and 2 alone, we cannot obtain the rest of the path. This is called by Barbour the "two-snapshots problem". The four pieces of data still needed for determining the path are concerned with the angular momentum (3 data) and the kinetic energy (1 datum), and that's why Newton needed the absolute space and time. Then how should we overcome this difficulty within the Machian frame?
Intrinsic Difference and Best Matching
The idea Barbour invokes is that of optimization. In the Newtonian mechanics, the principle of the least action is known. In figurative terms, "Nature explores all possibilities and selects something like a shortest path" (Barbour 2000, 112), but in order to define such "least action", the invisible framework of absolute space and time plays an essential role (the kinetic energy is essentially involved). In the Machian framework, however, such notions must be defined, if definable at all, in terms of the real or intrinsic features of configurations. Thus Barbour (together with his collaborator, Bruno Bertotti) tries to define a "distance" (and hence something like "geodesics") between neighboring points in Platonia, in such a manner.
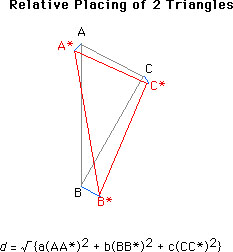
The rough idea is this: Suppose two triangles ABC and A*B*C* are placed relative to each other (the former is fixed, and the latter is placed relative to it), as in the Figure. This time, since we are considering dynamical problems, we have to assign a mass to each point; so let it be a, b, and c, respectively (thus a triangle now corresponds to a matter distribution in the universe). Then the trial distance d between the two triangles is defined as in the Figure.
This quantity d is of course an arbitrary quantity, although it does not presuppose the absolute space and time. However, Barbour points out that "it ... is possible to consider all relative positionings and find the one for which d is minimized" (Barbour 2000, 116). This minimum value is the intrinsic difference between the two matter distributions represented by the two trialgles. This is completely determined in Platonia, without relying on any external structure like absolute space. And this special positioning with the minimum value may be called the best-matching position. In this way, we can define "shortest paths" and these are "histories" in Platonia. The actual procedure is more complicated, but we do not have to worry.
But what is the relevance of all this to the previous two-snapshots problem? Here is Barbour's answer:
I think you will agree that finding shortest paths in an imagined timeless landscape bears little direct resemblance to our powerful sense of the passage of time. Yet the outcome turned out to be remarkably like what happens in Newtonian theory. ...
Any continuous path in it corresponds to a squence of triangles: they are the 'points' through which the path passes. But this is very similar to what comes out of Newtonian theory ...--which, however, yields not only the triangles but also their positions in absolute space and separations in time. ... Thus, as far as observable things are concerned, both theories yield the same kind of thing--sequences of triangles. The question is, what kind of sequences do the two theories yield? ...
The major difference is that the Machian theory makes more definite predictions. As a theory of geodesics, it determines the shortest path between any two fixed points in Platonia. It covers Platonia with such paths. These geodesics have the following important property: at any one point in Platonia, many of them pass through it. In fact, for every direction that you can go from a point, there is just one geodesic. This is the crucial difference. ...when the Newtonian histories are represented as paths in Platonia, it turns out that many can pass through the same point, and have at that point the same direction. However, these paths then 'splay out' and go to quite different places in Platonia. In Newtonian terms, they differ in energy and angular momentum. The difference is not apparent in the initial point and direction, but comes to light dramatically in the later evolution of the paths. This defect is absent in the Machian theory. (Barbour 2000, 118)
To be more specific, the unique Machian history (with a given direction through a point) is identical to one of many Newtonian histories; it is the one for which the energy and angular momentum are both exactly zero (119).
Barbour draws a remarkable consequence from this.
... in a universe which, like ours, contains many bodies, there can be innumerable subsystems that are effectively isolated from one another. this is true of the solar system within the Galaxy, ... Each subsystem, considered by itself, can have non-zero energy and angular momentum. However, if the universe is finite, the individual energies and angular momenta of its subsystems can add up to zero. In a universe governed by Newton's laws this would be an implausible fluke. But if the universe is governed by the Machian law, it must be the case. It is a direct consequence of the law. What is more, the Machian law predicts that in a large universe all sufficiently isolated systems will behave exactly as Newton predicted. In particular, they can have non-zero energy and angular momentum, and therefore seem to be obeying Newtons's laws in absolute space and time. But what Newton took to be an unalterable absolute framework is shown in the Machian theory to be simply the effect of the universe as a whole and the one law that governs it. (Barbour 2000, 119)All right. I will stop here. Although I have covered only one third of Barbour's book, it should be clear by now that this book is quite worthwhile for students of space and time. Moreover, Barbour continues to go on to general relativity (he argues that its deep structure is timeless and Machian) and quantum mechanics (if it aims at quantum cosmology, it must be timeless, Barbour argues, and the wave function Ψ of the unvierse is in terms of its relative configuration), after this. This is truly an original book.
ReferencesBarbour, J. B. and Bertotti, B. (1982) "Mach's Principle and the Structure of Dynamical Theories" Proceedings of the Royal Society of London A382 (1982), 295-306.
Barbour, J. B. (1982) "Relational Concepts of Space and Time" British Journal for the Philosophy of Science 33 (1982), 251-274.
Barbour, J. B. (1989) Absolute or Relative Motion? Vol. 1 The Discovery of Dynamics, Cambridge University Press, 1989.
Barbour, J. B. (1995) "General Relativity as a Perfectly Machian Theory", in Barbour and Pfister, eds., Mach's Principle (Einstein Studies, vol. 6), 214-236, Birkhaeuser, 1995.
Barbour, J. B. (1999) "The Development of Machian Themes in the Twentieth Century", in Butterfield, ed., The Arguments of Time, 83-109, Oxford University Press, 1999.
Barbour, J. B. The End of Time, Phoenix, 2000.
Earman, J. (1989) World enough and Space-Time, MIT Press, 1989. [See pp. 92-96 for criticisms of Barbour & Bertotti theory up to 1982; Barbour 2000 sketches how to extend the idea to field theories and quantum mechanics.]
Last modified Dec. 1, 2008. (c) Soshichi Uchii