![]()

|
How do you get this Bull's Eye? ª@ ª@ ª@ Original Figure in Perrin's Atoms |
 |
How do you get this Bull's Eye?
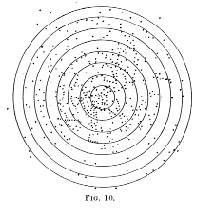
On p. 226 of Mayo's book, she shows a figure (7.2) where 500 points are distributed on the bull's eye; this figure is reproduced from Perrin's Atoms, p. 118, Fig. 10. Since Mayo's explanation is short, many readers (who are unfamiliar with experiments and manipulations of experimental data) may wonder how this figure is obtained. The point at issue is that how we can verify the assumption that the Brownian motion is "entirely irregular". Here is the original text (by Perrin):
Another and still more striking verification, which was suggested to me by Langevin, is obtained by shifting the observed horizontal displacements in directions parallel to themselves, so as to give them all a common origin. The extremities of the vectors obtained in this way should distribute themselves about that origin as the shots fired at a target distribute themselves about the bull's eye. This is seen in the figure given below (Fig. 10), on which 500 of my observations with grains of radius .367°æ are recorded; positions of grains were noted every 30 seconds. (Perrin, Atoms, 118)
I will show, in a rough outline, starting from "raw data", how you arrive at the bull's eye figure. See the folllowing chart. Notice that each of the "raw data" (1)-(3) may become more complex, if the timing of each step is shortened (e.g., if you record positions every 20 seconds, the path becomes more ragged). If we may take Perrin's words (in the last sentence) literally, he recorded the displacement of a grain only once (in this case), after 30 seconds, so that each vector comes directly from the datum. As regards the nature of "500 observations", he does not say anything; they may be observations of a single grain (in 500 steps), or observations of a number of similar grains. The presumption is that the conclusion is not affected in either case.
Last modified Jan. 27, 2003. (c) Soshichi Uchii