

Exact Formulation of the General Principle of Relativity?
Section Twenty-Eight
This section is quite important, in order to understand the meaning and significance of Einstein's "general principle of relativity". In section 18, Einstein formulated it thus:
(1) All bodies of reference K, K', etc., are equivalent for the description of natural phenomena (formulations of the general laws of nature), whatever may be their state of motion.
But now Einstein says that this actually does not hold. Instead, he says that the following should replace it:
(2) All Gaussian co-ordinate systems are essentially equivalent for the formulation of the general laws of nature.
This condition is called, in a technical word, the general covariance. As we have already seen, the laws of motion and electromagnetism did not change under the Lorentz transformation; that is, if we replace x, y, z, and t (coordinates of one inertial system K) by another set x', y', z', and t' (coordinates of another inertial system K'), these laws kept the same form and content. In other words, these laws are covariant under the Lorentz transformation. The new principle (2) requires a similar property with respect to any transformation (which must be smooth and continuous), any kind of choice of coordinate systems, and that is general covariance.
Although Einstein himself and many other physicists and philosophers were misled by the notion of general covariance, it is now widely recognized that there are actually two different things going on in the name of the general principle of relativity. One is the mathematical condition for a formulation of a theory, such as the special relativity, the Newtonian mechanics, or even the Euclidean geometry (considered as a physical geometry); and another is the content of such a theory, the elements kept invariant under such a transformation.
To make things more specific, the spatial distance between any two points is invariant under the Galilean transformation, but not under the Lorentz transformation. And the Euclidean geometry is a theory which keeps this content; the Lorentz geometry of special relativity has a quite different content, in that it requires the invariance of spacetime interval under the Lorentz transformation. However, keeping such a specific content intact, it is possible to give a covariant formulation of any such theories. Take the Euclidean geometry, for instance. It is usually formulated in terms of a Cartesian coordinate system (standard formulation), but it is clear that the same content can be presented in another formulation, say, in terms of a Gaussian coordinate system, where any axis may be curved, not straight, and two axes are not orthogonal. See the following figure.
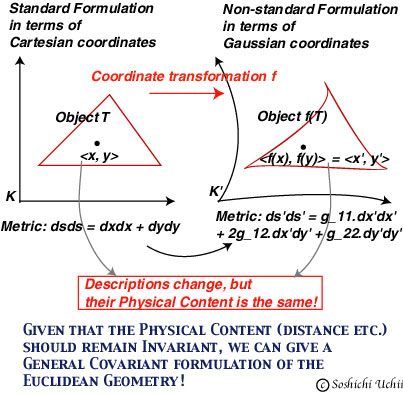
This clearly shows that the requirement of general covariance is a mathematical condition for a formulation of a theory, and it has, by itself, nothing to do with the physical content of the theory. Now, what is the essential difference between special relativity and general relativity as a physical theory? The answer seems clear: General relativity has a richer content than special relativity, in that it can treat gravitational fields of various kind. The difference lies in content, not in the manner of formulation. Thus if Einstein means by "general principle of relativity" the condition of general covariance, it is off the mark. The content of general relativity is condensed into Einstein's field equations, which have far richer contents both conceptually and empirically than special relativity, and contain special relativity as a limiting case. General relativity holds both for inertial and non-inertial systems, and there is no priviledged frame; whereas special relativity is limited to inertial systems, and hence it requires priviledged frames.
See General Principle of Relativity and Genesis of General Relativity (7).
Last modified, May 24, 2002. (c) Soshichi Uchii
suchii@bun.kyoto-u.ac.jp