


Schwarzschild Geometry
I have asked questions about general relativity of several experts in the field. With one exception, every single expert has started answering my question by writing down a tensor. That one exception is John Archibald Wheeler. (Edwin F. Taylor, "The Boundaries of Nature: Special & General Relativity and Quantum Mechanics, A Second Course in Physics", 6 January 1998, p. 2; see http://www.eftaylor.com/pub/oersted.pdf)
Schwarzschild Geometry
1. Preliminaries
Everyone will agree that no one can have a glimpse of general relativity without understanding Schwarzschild Geometry, the geometry around a star, heavy and light, and around a black hole. Fortunately, we can understand this geometry without getting involved in a tensor calculus.
Karl Schwarzschild (1873-1916), a German astrophysicist, gave the first rigorous solution (1916) to Einstein's field equations. He considered a static star (spherical, with no spin, and density is uniform). His solution was for the exterior of such a star (a solution for the interior was obtained later). Let us see some of the essential features of his solution, and the so-called Schwarzschild Geometry based on it. This solution is applicable, as a good approximation, to the sun, the earth, and a black hole (without spin) as well (although, of course, Schwarzschild did not know "black hole", and Einstein and Eddington tried to disregard such a possibility). The following exposition owes a great deal to Taylor and Wheeler (2000), chapter 2 (although figures are mostly mine).
First of all, you have to realize the implication of general covariance. General relativity is the first theory which satisfied general covariance, and this roughly means that physical laws do not depend on our choice of a coordinate system; essential physical quantities are invariant, independent of a choice of coordinates. Thus we can choose, for studying the geometry of a given spacetime, a coordinate system most convenient for our purpose. Change or choice of a coordinate system is of course possible for other classical theories such as Newtonian mechanics (e.g., Cartesian coordinates as well as polar coordinates are possible), but general covariance allows more freedom. But for present purposes, we do not have to discuss this. What is important is that polar coordinates are most convenient for Schwarzschild Geometry, since the mass of a spherical star has a unique center. In the following figure, you can see a two dimensional slice of a polar coordinate system; notice that this is an equatorial plane of the given star (see Embedding Diagram). It may be regarded as a cross section of a number of (imaginary) concentric spheres sorrounding the star.
However, unlike the case of Newtonian mechanics, we have to be careful about the presuppositions of such a coordinate system, since in general relativity various reference frames are possible and allowed. How should we choose axes of a coordinate system, and how should we obtain a value on such an axis? How should we measure time? It is essential, in relativity theories, we distinguish between "coordinate time" (value of time on the time axis) and "proper time" (time measured along a given world line), since the latter changes depending on motion (but it is one of the invariant quantities).
(1) Angles °î (at the center) can be obtained, given two lines making an angle at the center of the star, as in Euclidean geometry. We will call such a value, "°î-coordinate".
(2) Distance r must be obtained as follows. Given a point outside of the star, first measure (by means of the standard rod available at each location) the circumference C of the circle crossing the point on an equatorial plane; then
r = C/2°ë.
This is the r-coordinate (called also "reduced circumference" by Taylor and Wheeler) of the point (and of the circle or sphere); don't think that this value can be directly used for determining the geometric distance between two points on the same radius. A coordinate-value is one thing, and a distance or an interval is quite another thing in relativity; the gap becomes most conspicuous with time--the coordinate time vs. the proper time, the former measured by far-away clock (unaffected by gravity), the latter by a local (but the same standard) clock (affected by gravity, seen from a far-away observer). In order to connect the two, we need metric, which in turn can be derived from Einstein's field equation, given appropriate initial and boundary conditions; but following Taylor and Wheeler (2000), we begin with metric, disregarding the original field equation. As is suggested by this, Schwarzschild coordinates r, °î, t are for overall bookkeeping, so to speak, translating and unifying various measurements made by local observers. The "rules of translation and unification" are provided by Schwarzschild metric.
(3) Another presupposition is that mass is measured in units of length (just as time can be measured by the length light travels in that time); this way the metric and geometry become simpler. We will signify the mass of the given star by M, with this understanding.
(4) Finally, we have to notice the boundary conditions for Schwarzschild's solution. A single static star is located in an overall Minkowskian spacetime; this, in particular, means that the metric is Minkowskian in far-away regions. The spacetime there is flat, and (practically speaking) only limited portion around the star is curved according to Schwarzschild metric, which we will see shortly. Thus the overall view of Schwarzschild Geometry is as in the following figure (the region of Schwarzschild Geometry may change, practically, depending on the the mass of the star, and on the purpose of investigations; theoretically, spacetime becomes flat only at infinity). The gravitational field (and hence curvature of spacetime) is generated by the star at the center (the origin of the preceding polar coordinates), and this determines the geometry around the star.
2. Schwarzschild Metric
"... but when the Rabbit actually took a watch out of its waistcoat-pocket, and looked at it, and then hurried on, Alice started to her feet, ..." (Alice's Adventures in Wonderland)
Taylor and Wheeler nicely introduce the notion of metric, following the beginning part of Alice in Wonderland. The White Rabbit, running with a watch, measures his time by his watch, and this time is his proper time. For present, let us assume he runs in a straight line with a uniform speed (and, in addition, he carries a standard rod, instead of an umbrella!). Further suppose Alice stays at rest and measures time and distance by her own clock (synchronized with the Rabbit's watch) and rod (of the same brand as Rabbit's rod).
Suppose Rabbit's watch ticks twice as he runs; then how do these two events look to Rabbit and Alice? According to special relativity, as in the following figure, the Minkowski metric relates Rabbit's proper time with Alice's time and space, in the Minkowski (flat) spacetime. Time is assumed to be measured in meters, that is, the usual time multiplied by the velocity of light (thus light cone makes an angle of 45 degrees to the time axis and to the spatial axes).
It should be noted that proper time is invariant, i.e. the same for Alice and Rabbit, or for any inertial observers (moving with a uniform velocity to each other). The same can be said about proper distance, i.e., the spatial distance between two events simultaneous for Rabbit, say (I will omit the explanation of simultaneity, since you are already familiar with it). Suppose two firecrackers explode simultaneously, for the running Rabbit, at the top and the bottom of the rod he carries.
In this case, since the time separation (for Rabbit) between the two events becomes zero, the proper time is also zero, and instead, the proper distance °Ü is related to other observer's time and distance (for Alice, time separation t between such two events is not zero) as in the following figure, which is another aspect of the same (Minkowski) metric; this proper distance is also invariant.
So far we talked about the Minkowski metric in a flat spacetime. With this preparation, we now proceed to Schwarzschild metric in a curved spacetime. Also, we have to remember that we move from Cartesian coordinates to polar coordinates. So let us see how the proper distance looks like in polar coordinates. A small distance ds, on a two dimensional flat space, satisfies the Pythagorean theorem, and the same distance can be expressed in terms of polar coordinates as in the following figure (adapted from Taylor and Wheeler 2000, Figure 5).
This relation holds in a flat spacetime, and substituting this (for the square of s) in the preceding metric, we can easily obtain the metric expressed in terms of polar coordinates. And it is customary for physicists to omit all parentheses from such expressions. Thus the metric, now for a tiny quantity with d, and in terms of polar coordinates, is as follows:
And now we finally come to Schwarzschild metric. Schwarzschild metric, for proper time (or timelike, in technical term) and for proper distance (spacelike). The difference from the preceding flat case is that the first two terms have the "curvature factor" so to speak:
As we have remarked already, this metric is obtained from Einstein's equation; but for Schwarzschild Geometry, this metric is the basis of everything. We can show how space and time are curved, according to this metric.
You may wonder where on earth we get this metric. As I said, in a word "from Einstein's field equations"; but those who want to see a more detailed answer, but without getting into a messy tensor calculus, should read Wheeler (1999), chapters 6-9. I know of no better readable exposition of the field equations and their relation to Schwarzschild metric; it's enjoyable yet keeps sufficient rigour.
Time Warps
Even at a glance, we can see that the proper time °„ at some location close to the star is smaller than the far-away (coordinate) time t, because the curvature factor is smaller than one (and notice that the difference of r-coordinate is zero for two events--two ticks of the clock--at the same spatial location). As a direct consequence of this, the frequency of light signal emitted from such events looks smaller to far-away observers; in other words, far-away observers see longer wave length, and that is nothing but the "red-shift" by gravity. That is to say, time is warped, and more so, at a closer location to the star.
The light from the star has a lesser frequency for the far-away observer.
Now, what if r approaches 2M? The local proper time °„ becomes smaller and smaller compared to the far-way time t, and approaches 0. Thus one tick of the clock close to this distance takes, according to the far-way clock, almost an infinite time! Time warps so much. The sphere of this radius 2M is called horizon; a signal from the horizon takes an infinite time to reach (in other words, never reaches) the faw-away observer.
Space Warps
Then what about space, or proper distance? This can be seen from the distance version of the metric; now you may disregard the first term, since time is freezed, giving an instantaneous space. Let us consider a black hole, the most extreme case of space warps (it has a singular point at the center, all matter absorbed into that point). The top figure is an embedding diagram (the space slice is 2-dimensional, but in order to visualize its curvature, this slice is embedded in a 3-dimensional Euclidean space). The bottom figure, from the top and a cross section (the curve is a parabola). Remember that only the paraboroidal surface has physical meaning (figures adapted from Taylor and Wheeler 2000, Figures 6 and 7).

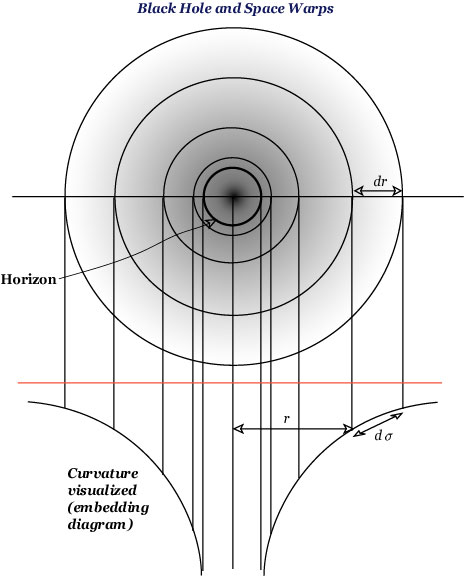
Horizon is where r = 2M, and there the ratio d°Ü/dr becomes infinite. As is explained in many popular expositions, nothing, including light, can get out of the horizon. Thus you cannot see the inside of the horizon. As regards proper distance °Ü, you may notice that its value becomes larger and larger as compared to r, as you approach the horizon. Space warps this way. The deflection of star light around the sun (the famous prediction by Einstein, confirmed in 1919) can be explained in terms of space warps and time warps. For more of Schwarzschild Geometry, see Taylor and Wheeler (2000) and other books.
Schwarzschild geometry (a spatial slice, an equatorial plane) around the sun looks like this. The white part is in the interior of the sun, to which Schwarzschild interior solution applies.
References
Taylor, Edwin F. (1998) "The Boundaries of Nature: Special & General Relativity and Quantum Mechanics, A Second Course in Physics", 6 January 1998. See http://www.eftaylor.com/pub/oersted.pdf
Taylor, Edwin F. and Wheeler, J. A. (2000) Exploring Black Holes, Addison Wesley Longman, 2000.
Thorne, Kip S. (1994) Black Holes and Time Warps, Papermac, 1995. [öMö—1997]
Wheeler, J. A. (1999) A Journey into Gravity and Spacetime, Scientific American Library, 1999.
Last modified February 5, 2003. (c) Soshichi Uchii