![]()
 |
ヘンペルのカラスのパラドックス The Raven Paradox
『科学哲学入門』 6.6 への補足
Hempel (1945) presented the following paradox of qualitative confirmation.
Suppose you wish to confirm the hypothesis:
(1) All ravens are black.
This hypothesis is logically equivalent with:
(2) All non-black things are non-ravens.
Now, it seems quite reasonable to assume that if any evidence supports (1), it also supports (2), because the two hypotheses have the same content.
All right, then, how do you try to confirm (1)? Of course, you may try to catch a raven, and to examine its color; thus you will confirm (1) by black ravens, provided that you found no non-black ravens. Fine. But by the parity of logic, you will try to confirm (2), by catching a non-black thing and examining whether it is non-raven; thus you will confirm (2) by non-black non-ravens. OK?
But recall that (1) and (2) are logically equivalent. Then we have to admit that hypothesis (1) is also confirmed by non-black non-ravens! Thus, if you find a red chalk, or a green emerald, these will confirm that all ranvens are black. Are you happy with this? If not, where did we go wrong?
The morals of this paradox seems to be that our qualitative intuition of confirmation is not reliable; and moreover, our intuitions may be presupposing tacit assumptions. For another thing, we may well be unable to distinguish zero-confirmation from a very small degree of confirmation in our qualitative judgment of confirmation. Thus one way to solve this paradox seems to be to try to construct a quantitative model of confirmation, by making explicit all assumptions contained in our examples.
Try a Gedankenexperiment with the following two worlds: you are supposed to be trying to confirm hypothesis (1) in each world. In the world of Fig. 1 (world 1), would you like to catch ravens and examine their color? What if you try to confirm (1) in the world of Fig 2 (world 2)? Which world is closer to our world?
Fig. 1 The world with overwhelmingly many black ravens
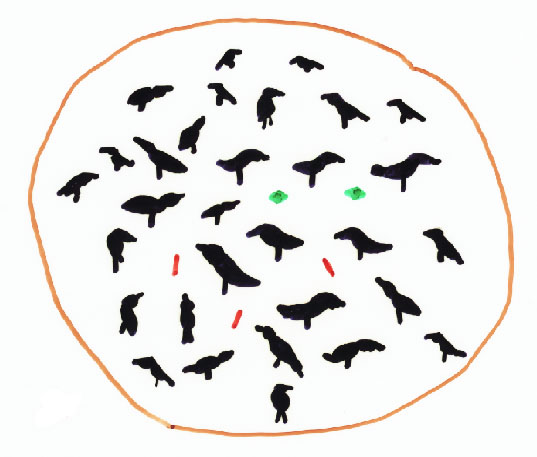
Fig. 2 The world with very few black ravens
The Carnapian quantitative model of confirmation enables you to see the quantitative difference of degrees of confirmation by each type of evidence, either in world 1 or in world 2. The same can be accomplished in the Bayesian models too.
Last modified April 11, 2002. (c) Soshichi Uchii