![]()
水星の近日点移動
テキストでも触れたとおり、海王星の発見に大きな貢献をしたルヴェリエは、水星の近日点移動の問題にも気づき、この問題を解決するための仮説を模索し計算をおこなったが、水星の内側に新たな惑星は発見できなかった。
Urbain Leverrier (1811-1877)
[picture from a French stamp]
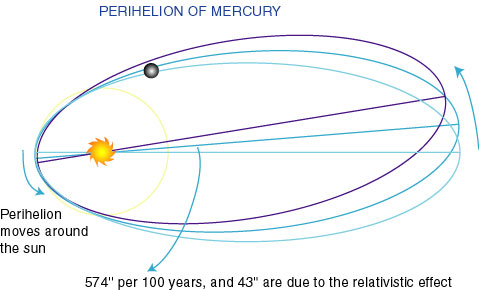
近日点とは、惑星が公転軌道上で太陽に最も近づく位置のことであり英語では perihelion と呼ばれる(図を参照)。観測値から割り出された水星の近日点移動の大きさは、百年につき角度にして570秒あまりで他の惑星に比べて格段に大きく、十分観測にかかる大きさなので(他の惑星の近日点移動ははるかに小さい)天文学上の問題とされたのである。ルヴェリエの計算によれば、このうち38.3秒の分だけがニュートン力学に基づく計算値によっては説明できないで残るとされた。現代の値は、百年当たり574秒の移動のうち、ニュートン力学で説明できない分は43秒ということになっている。以下の図では、この数値のみを記入してあるので誤解のないように注意されたい。
この問題の解決は、数十年後に意外な形でえられた。特殊相対論に満足できず、重力の扱いについて一般相対性理論を目指して格闘していたアインシュタインは、1915年11月18日に、彼の重力場の方程式から水星の近日点移動が定量的に予測できることを発見した。水星は太陽の重力場の影響を最も強く受け、軌道が円から楕円にはずれる度合いが大きいので、近日点移動が大きくなるはずである。水星のその予測された移動の量は、ルヴェリエ以後の研究でも説明不可能と見なされた43秒の分まで観測値とほぼぴったりと一致していたのである。これに加え、重力による光の彎曲と、赤方偏移(光の波長が長くなること)とが理論的に予測された(こちらについては、アインシュタインはすでに8年ほど前から気づいていた)。
理論と観察の関係を分析するという文脈でこの例を見るとき、どういう注意が必要だろうか?一つのポイントは、一般相対性理論からの、一つの具体的な予測が観測と一致したということ。これは、一般相対性理論の全体が確証されたことを意味するわけではない。もう一つのポイントは、近日点移動の観測上の大きさがどのように確定されるかということ。これは、メイヨー言うところの「実験的知識」に属する事柄で、ひところの「新科学哲学」の論者が言い立てたように、理論先導でいくわけではない。むしろ、実験的知識には、それ自体の自律的な「確証の論理」があって不思議ではない。1919年の、イギリス観測チームによる太陽の周りでの光線の湾曲の確証についても同様であり、実際の手続きにある程度立ち入った分析を踏まえてものを言わなければならない。予測は理論先導でも、だからといって予測の確認手続きまで理論先導になるわけではない。
文献
パイス『神は老獪にして・・・』産業図書、1987、331-334ページほか。
Einstein, A. Relativity: the special and the general theory, Three Rivers Press, 1961, pp. 143-145.
Earman, J. and Janssen, M. "Einstein's Explanation of the Motion of Mercury's Perihelion", in Einstein Studies vol. 5, The Attraction of Gravity (ed. J. Earman, M. Jenssen, and J.D. Norton), Birkhaeuser, 1993, 129-172.
Mayo, Deborah Error and the Growth of Experimental Knowledge, University of Chicago Press, 1996.
スターシェル「相対性理論の歴史」『20世紀の物理学』vol. 1、丸善、1999、312-313ページ。
Last modified, March 26, 2003. (c) Soshichi Uchii