Newtonian Mechanics

Newtonian Mechanics

ニュートンの運動法則（『自然哲学の数学的諸原理』1687、河辺六男訳、中央公論社、世界の名著『ニュートン』所収。）

法則 I　すべて物体は、その静止の状態を、あるいは直線上の一様な運動の状態を、外力によってその状態を変えられないかぎり、そのまま続ける。

法則 II　運動の変化は、及ぼされる起動力に比例し、その力が及ぼされる直線の方向に行なわれる。

法則 III　作用に対し反作用は常に逆向きで相等しいこと。あるいは、二物体の相互の作用は常に相等しく逆向きであること。

これらの法則は、別名でそれぞれ「慣性の法則」、「運動方程式」、「作用と反作用の法則」と呼ばれることもある。これに、

万有引力の法則 　F = G(mm'/rr) [mとm'は二質点の質量、rは両者の間の距離、Gは定数]

が加わることにより、ニュートン力学の基本法則が出そろう。

とくに解説を要するのは第二法則である。現代の力学の教科書では、力をF、質量をm、加速度をaで表して

(1) F = ma

と書かれることが一般的である（比例定数は単位の取り方によって1にできるので省略される）。さらに、加速度aは速度vの変化（速度の微分、dv/dt）、速度vは位置xの変化（dx/dt）だから、結局、加速度は位置の2階の微分となって

(2) F = m(dv/dt)

と変形できる。これが運動方程式と呼ばれ、力学の問題を表す基本形式となる。「運動方程式を解く」とは、この微分方程式を積分していくことにより、たとえば粒子や惑星の運動の軌跡を求めることを意味する。具体例を挙げるなら、太陽の周りの火星の軌道が楕円になること（ケプラーの第一法則）は、太陽からの引力により力Fが決まり、火星の質量がわかれば運動方程式が書けることなるから、あとは適当な時点での火星の位置と初速（慣性の法則に従った直線運動の速度）がわかれば、積分を行なって火星の軌道を求める、という手続きによって導かれる。以上の手続きを図解してみよう。

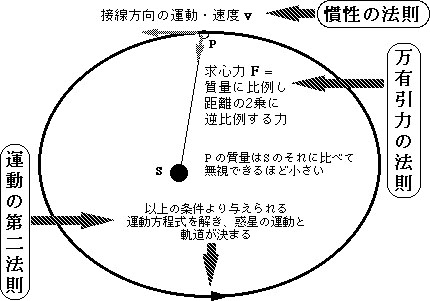
各々のステップが積み重なっていく様子も図示してみよう。

ただし、現代では普通のこのやり方は、ニュートン自身が採った方法ではない。彼は、徹頭徹尾幾何学的方法で力学の問題を解いた。微分方程式を立てて力学問題を解くというやり方は、18世紀にオイラーらが始めた方法であり、ニュートン自身が述べた第二法則には、このやり方は示唆されてないのみならず、式さえ書かれていないのである。もっと詳しくは、伊藤和行「古典力学における運動法則の歴史性」『哲学研究』570号、2000年を参照。

第三法則については、これまでの説明で言及の必要がないように見えるかもしれないが、実はそうではない。惑星の質量が太陽のそれに比べて無視できるほど小さいと仮定したので、この法則を無視できただけの話である。「作用と反作用」ということで、「わたしが手で壁を押す、わたしの手が壁から圧力を受ける」というようなことだけを連想してはならない。運動の文脈では、相互作用による運動量（質量と速度との積）の出入りが問題とされるのである。例えば、もっとも単純に二つの質点（質量ｍとn）だけの相互作用に話を限るなら、第二の質点から力を受けて第一の質点に運動量の変化が生じたなら、第二の質点の方には逆向きの運動量の変化が生じて、全体としては運動量の変化は相殺される、というのがニュートンの意図した意味である。前述の惑星運動の例では、第三法則ももちろん働いているのだが、太陽の運動量の変化は近似的に無視できると見なして計算を進めたということである。