

Hawking, A Brief History of Time, Short-Short!
Hawking, A Brief History of Time (1988, Japanese tr. by H. Hayashi, 1989, 1995), Short-Short!
[一時ベストセラーになったホーキングのこの本は、量子宇宙論の流れをつかむには有用であり、時空の哲学にも大いに関わりが深い。ただし、細部を埋めるためには自分で適当な文献を勉強して補わなければならない。]
現代の宇宙像は、アメリカの天文学者エドウィン・ハッブルがわれわれの銀河が唯一の銀河ではないことを証明した、1924年までしかさかのぼれない。事実、銀河は多数存在しており、広大かつ空虚な空間でたがいにへだてられている。このことを証明するために、ハッブルは銀河までの距離を決定しなければならなかった。(邦訳65)
ハッブルは他の銀河が存在することを証明したのち、何年間も銀河の距離のカタログづくりや、そのスペクトルの観測に打ちこんだ。その当時、大部分の人たちは、銀河がごく無秩序に運動していると考えており、当然青方偏移したスペクトルも赤方偏移したスペクトルと同じぐらいの割合で見つかるだろうと予想していた。そのため、大部分の銀河が赤方偏移を示しているとわかったときには、びっくりしてしまった。ほとんどすべての銀河がわれわれから遠ざかっているとは!だが、もっと驚くべきことがあった。それは1929年に明らかにされたハッブルの発見である。銀河の赤方偏移の大きさすら無秩序ではなく、その銀河とわれわれの距離に正比例している。・・・これは、宇宙がそれまでだれもが考えていたような静的なものではなく、膨張していることを意味する。(邦訳69)
・・・静的宇宙に対する信仰はあまりにも強く、20世紀初頭までも残存した。アインシュタインでさえ、1915年に一般相対性理論を定式化したときには、宇宙は静的であるはずだと思いこんでいたために、理論を修正して方程式の中にいわゆる宇宙定数を導入し、宇宙が静的になるように仕組んだほどだ。彼は新しい”反重力”を導入したが、これはなんら特別な源ももたず、ただ時空構造そのものの中に組みこまれたものだった。時空には膨張する傾向が内在しており、これは宇宙のすべての物質の引力とちょうど打ち消し合うようになっているので、その結果静的宇宙が生じるとアインシュタインは主張した。一般相対性理論の価値を額面どおり受け取ろうとしたのは、どうやら一人しかいなかったようだ。それはロシアの物理学者・数学者アレクサンドル・フリードマンである。アインシュタインやその他の物理学者が、非静的宇宙という一般相対論の予測を回避する道を探している間に、フリードマンは非静的宇宙そのものを解明しようとくわだてたのであった。
フリードマンは宇宙について非常に簡単な仮定を二つ設けた。われわれがどの方向をながめても宇宙は同じように見えること、そして、別のどんな場所からながめても同じことが言えるだろうという仮定である。フリードマンはこの二つの考えだけから出発して、宇宙は静的であると予想すべきではないことを示したのだった。事実、エドウィン・ハッブルの発見に数年先立つ1922年には、フリードマンはハッブルの見いだしたことをすでにすっかり予測していたのである!(邦訳70-71)
フリードマン解はすべて、ある一つの特徴を共通にもっている。それは過去のある時点(100億ないし200億年以前)には、隣りあう銀河の間の距離はゼロだったはずだということである。ビッグバンとわれわれが呼ぶその時点には、宇宙の密度も、時空の湾曲率も無限大だっただろう。数学では無限大の数を本当は扱えないのであるから、このことは、一般相対性理論(フリードマン解はこれにもとづいている)が、宇宙にはこの理論自身が破綻するような一点が存在すると予測していることを意味する。このような点は、数学者が特異点と呼んでいるものの一例である。(邦訳79)
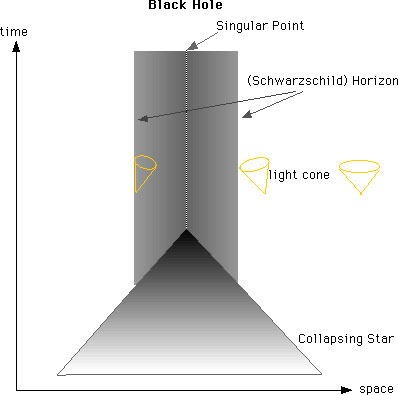
[ロジャー・ペンローズ]は一般相対性理論における光円錐のふるまい方と、重力がつねに引力であるという事実とをいっしょに用いて、自分自身の重力で崩壊していく星はある領域の中に閉じこめられるが、その領域の表面は最終的にはゼロに収縮していくことを示した。表面がゼロになれば、当然体積もゼロになる。星の中のすべての物質も体積ゼロの領域の中に圧縮されるので、物質の密度と時空の湾曲率は無限大になる。言いかえれば、ブラックホールと呼ばれる時空のある領域の中に、特異点が生じるのである。・・・ 1965年、私は、重力崩壊を起こしている物体はどんなものでも最後には特異点をつくるというペンローズの定理について読んだ。宇宙が現時点で大極的に見てフリードマン・モデルとほぼ同じであれば、ペンローズの定理で時間の方向を反転させたとき、彼の定理の条件は依然成立したまま、崩壊が膨張に変わることを私はすぐ見抜いた。ペンローズの定理は、崩壊するいかなる星も特異点に終わるべきであることを示していた。時間を反転させるという論法で、いかなるフリードマン流の膨張宇宙も特異点からはじまるべきであることが示されたのである。・・・
それから何年かの間に私は、特異点が存在しなければならないことを証明したこの定理からあれこれの条件を取り除くために、新しい数学的テクニックを開発した。その最終結果が1970年のペンローズと私の共著論文である。これは一般相対論が正しく、かつ宇宙が、われわれが現に有しているのと同じ程度の量の物質を含んでいさえすれば、ビッグバン特異点があったはずだということを最終的に証明したものだった。・・・私が見解を変えて、宇宙のはじまりには実のところ特異点がなかったということを、いまごろ他の物理学者に信じこませようとしているのは、たぶん皮肉なめぐり合わせだ──あとで述べるように、量子効果を考慮に入れると特異点は消え去るのである。(邦訳83-85)
[宇宙論のインフレーション理論と新インフレーション理論の解説が入るが、それは省略。インフレーションとは、加速度をもった膨張という意味であり、ビッグバン直後にインフレーションの(短い)期間を設定するのがインフレーション理論である。]
だが、特異点定理が本当に示しているのは、量子重力効果が大きな意味をもつほど重力場が強くなるということである。古典理論では、もはや宇宙はうまく記述できない。そこで、宇宙のごく初期の段階を論じるには、重力の量子論を用いなければならない。あとでわかるように、量子論では通常の科学法則が、時間のはじまりも含めていたるところで成立していることが可能である。量子論では特異点が存在する必要はないので、特異点に対する新しい法則を仮定することも必要でなくなる。(邦訳190)
実時空にもとづく古典的重力論では、宇宙には二通りのふるまい方が可能であるにすぎない。無限の時間にわたって存在してきたか、さもなければ過去のある有限の時刻に、特異点からはじまったかのどちらかである。これに対し重力の量子論では、第三の可能性が開かれている。この場合には、時間の方向が空間の方向と同じ性質をもつような、ユークリッド的時空を用いているので、時空は大きさが有限でありながら、しかも境界あるいは縁を形づくる特異点をもたないでいることが可能なのだ。・・・重力の量子論が開いてくれた新しい可能性では、時空は境界をもつ必要がないので、境界における時空ふるまいを特定する必要もなくなる。・・・だからこう言っていい。「宇宙の境界条件は,それが境界をもたないということだ」。宇宙は完全に自己完結しており、その外部のなにものにも影響されない。(邦訳193-194)
[「実時間と虚時間」というホーキングの有名な区別が出てくるが、これを理解するためにはミンコフスキー空間での「間隔」の定義を想起すればよい。直角三角形に関するピタゴラスの定理では、斜辺の二乗は他の辺の二乗の和に等しい。その和の平方根をとれば斜辺の長さが得られる。ところがミンコフスキー空間で二点間の間隔を同様に平方根で求めるときには、時間軸の値の二乗値を空間軸の二乗の和から引いて平方根をとる。つまり、実時間の値に虚数 i がかかるのと同じことになるので、平方根をとるときには、間隔を考える二事象の配置によっては、間隔が虚数値になる場合が生じる。これを防ぐためには、時間値を虚数で表せばよい。これによって時間軸は空間軸とまったく同等になる。単に数学的なテクニックだけの話ではなく、宇宙の初期にはそのように見なせる時期があったと想定する(そうすればいろいろな説明がうまくいくと考える)のがホーキングとハートルの理論である。以上の想定により、特異点からのビッグバンという描像に変わって、特異点をもたないなめらかな初期宇宙からのビッグバンという描像が得られる。簡単に言えば、一般相対論の実時間解、ド=ジッター宇宙(計量はローレンツ−ド=ジッター計量)の下半分に、虚時間解に対応するユークリッド的四次元球(計量はユークリッド計量で、ローレンツ−ド=ジッター計量の実時間の代わりに虚時間がはいる)の下半分をつなぐ、という描像である。次図参照。『時空の本質』112-113も参照。]

『ホーキング、宇宙を語る』(林一訳、早川文庫、1995)
『ホーキングとペンローズが語る時空の本質』(林一訳、早川書房、1997)See http://www.sciam.com/0796issue/0796hawking.html
(やや散漫なところもあるが、ポール・デイヴィス『時間について』(林一訳、早川書房、1997)も併せて読めばよいかもしれない。)
Last modified March 30, 2003.(c) Soshichi Uchii suchii@bun.kyoto-u.ac.jp