

Approaching the Horizon of a Black Hole
What is going to happen if you approach the horizon of a black hole?
In order to pursue consequences of Schwarzschild Geometry, let us imagine that a test particle approaches the horizen of a black hole. The particle comes from infinity, and its initial velocity is zero. What is going to happen with this particle, as it comes closer to the horizon? To see this, we need three kinds of frame: (1) Schwarzschild coordinate system, r, āė, t; (2) free-float system attached to the particle; and (3) coordinate systems each of which is on a concentric shell surrounding the black hole.
(2) and (3) are local frames, and each has its own rod and clock; although these rods and clocks are of the same brand, rods may change their length (proper distance), and clocks may change their pace (proper time), because of the velocity of the particle and gravitational fields around the black hole. And recall how r-āė-t coordinates of (1) are set, for the overall book-keeping; r is a calculated value, and t is measured by far-away clock.
Let us see the change of velocity of the particle, as it approaches the horizon. But we have to ask: which velocity, velocity according to which frame? First of all, velocity v according to (1) is obtained, from the Schwarzschild metric, as follows (for the process of derivation, see Taylor and Wheeler (2000), chapter 3):
(A) v = dr/dt = -(1 - 2M/r)üŃüi2él/r).
The minus sign means that the radial distance is decreasing. And, since the free-float frame is local, and it is useless for measuring its own speed, it needs something else relative to which it moves at some speed; for this purpose, we can use (3), i.e., a system of concentric shells. For when the particle passes a shell, measurements can be made on that shell, as regards the velocity of the particle relative to the shell, and the particle passes each shell consecutively. Thus we can obtain a series of values for the particle's local velocity, and we signify them by v_shell; it is obtained as follows (again, for derivation see Taylor and Wheeler, chapter 3):
(B) v_shell = (dr_shell)/(dt_shell) = -üŃüi2él/r).
To see the difference between (A) and (B), it is best to look at the following graph (adapted from Taylor and Wheeler, chapter 3, Figure 5).
You can clearly see the difference. The coordinate velocity v approaches zero, as the particle comes closer and closer to the horizon; whereas the v_shell approaches the velocity of light! Now, then, what really happens at the horizon? Is it the case that the particle can never cross the horizon, since v becomes 0 there? Or does it cross the horizon with the velocity of light? Well, does this question of "really" make sense? Before answering these questions, you should remember that Schwarzschild coordinates are artificial devices; (some) singularities appear because of the way these coordinates are set (Schwarzschild Geometry is primarily for studying the exterior of a star, you may recall). You should also remember that concentric shells cannot be constructed within the horizon. We need other frames for studying the crossing the horizon and motions within the horizon. One thing is certain: the particle can cross the horizon, but never again.
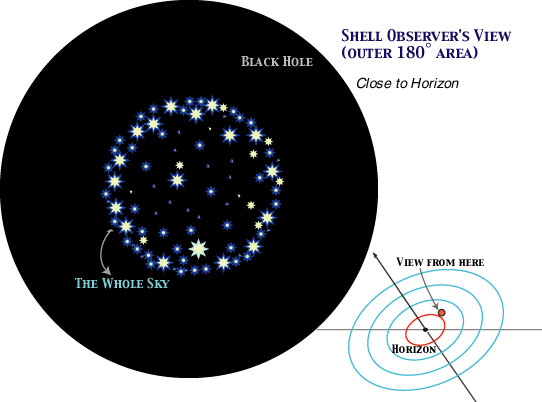
How does the sky look to the observer on a shell close to the Horizon? Here is an image (adapted from Thorne 1994, picture P. 4; see also Taylor and Wheeler, ch. 5, Figure 15), but remember this is a view from the observer at rest on the shell. An observer on a free-float particle (falling into the Black Hole) would have a different view (primarily because of aberration). Mathamtics for this is a bit complicated, and see chapter 5 of Taylor and Wheeler.
References
Taylor, Edwin F. and Wheeler, J. A. (2000) Exploring Black Holes, Addison Wesley Longman, 2000.
Thorne, Kip S. (1994) Black Holes and Time Warps, Papermac, 1995. [¢M¢¾1997]
Last modified Sept. 20, 2007. (c) Soshichi Uchii