

Seminar on Spacetime, 2003 Fall
by Prof. Soshichi Uchii
Part 2 The Invisible Framework and the Ultimate Arena
Part 2 is very important. You should obtain basic knowledge of classical physics (particle physics) in terms of the simplest example of a triangle formed of 3 mass points. The Newtonian framework presupposes external (absolute) space and time. Whereas the Machian approach, which Barbour recommends, can be developed in terms of Platonia (Triangle Land, for the 3 particles).
Since Barbour sometimes changes perspectives for presenting Triangle Land and Shape Spaces (which is a 2-dimensional part of Triangle Land, on which any motion can be represented, disregarding sizes and qualitatively), the uninitiated reader may be confused. Here are two basic figures, and by keeping them in your mind, you can avoid confusion.
This same Triangle Land, looked from another angle, appears as follows:
Red triangles (2-dimensional space) are what Barbour calls a Shape Space. Barbour often shows them from the reverse side (so the right and the left are reversed). Notice that any motion (continuous line in Triangle Land) can be projected (say, according to light emanating from the origin of the coordinates) on any of the Shape Spaces, so one can represent all.
Further, look at the black dot and its distance from each plane of the coordinate system, as indicated by italic orange letters. You can immediately see why
BC + CA = AB
holds on the top side of the largest Shape Space.
Further, take any one of the shape spaces. It has the following nice property.
Å@

Assignment, due November 7 (Fri). See this.
See the following:
Kinetic Energy and Potential Energy
For the Two Snapshots Problem, The Machian Problem
One datum of the kinetic energy of the whole system (in other words, the velocity of the center of mass of the system), and three data of the angular momentum (3 independent directions; i.e. the triangle rotates around an axis, and this rotation has three components) are needed in the usual Newtonian mechanics (Poincare was the first to point this out clearly). Does this show that absolute time and space are necessary for mechanics?
Tait's Inertial Clock (pp. 100-103) is quite instructive.
Suppose Newton claims that three particles, 1, 2 and 3, are moving purely inertially and that someone takes snapshots of them. These snapshots show the distances between the particles but nothing else (except for marks that identify the particles). We know neither the times at which the snapshots were taken nor any of the particles' positions in absolute space. (Barbour, 100)Barbour's Figure 20 (p. 102), however, is not quite good, since it is depicted in grey scale. Instead, see the following, a multi-color version.
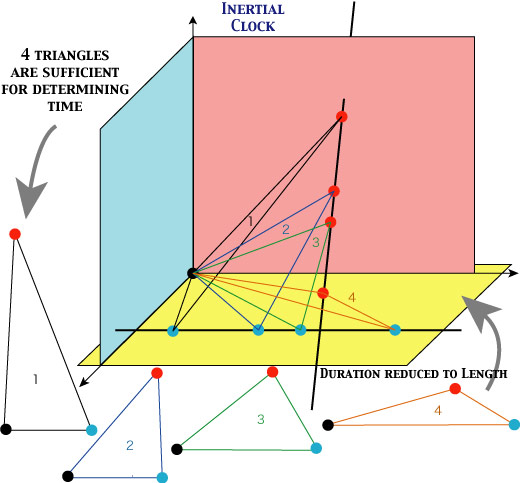
Thus, four snapshots will give eight useful data, seven of which will establish the Newtonian frame into which the triangles fit, while the remaining one will verify that they are indeed obeying Newton's law. (Barbour, 102)
According to Barbour's reconstruction of the Machian mechanics (classical), the whole universe has a zero energy and zero angular momentum (for, there is nothing relative to which it moves or it rotates). See pp. 118-9.

Then, each relatively isolated system looks as if it is moving relative to a fixed framework, absolute space and time, as Newton said. However, according to the Machian mechanics, the law of the whole universe determines motion as well as a framework (space and time).
2nd Assignment, due Dec. 5 (Fri). See this.