

Seminar on Spacetime, 2003 Fall
by Prof. Soshichi Uchii
First Assignment, due Nov. 7 (Fri)
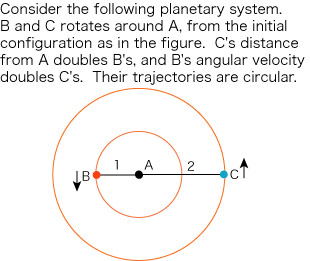
For the preceding system, draw the path of the system in Triangle Land. You may consider only one cycle, i.e. B's two revolutions and C's one revolution. Be sure to draw several triangles, which you regard as important for representing crucial positions. You may plot the path either in the 3-dimensional Triangle Land itself or in a 2-dimensional Shape Space. Don't forget to add appropriate explanations for your drawing!
Essentials: Notice AB and AC are constant through all the movements. This means that the trajectory is on both of the planes where AB=1 and AC=2 in Triangle Land. Depict this trajectory (which is a straight line) and project it onto an appropriate Shape Space, and the following figure is obtained (the red line is the trajectory).
Notice that we cannot distinguish two triangles which are a mirror image of each other; they are identical in Triangle Land and Shape Space (Identity of Indiscernibles). Thus one revolution of B (and a half for C, which means CBA on the same line in this order) is enough for determining the trajectory; the rest is just a mirror image and hence identical in the reversed order.