Index Page

Seminar on Spacetime, 2003 Fall

by Prof. Soshichi Uchii

Since Part One is mostly sketchy, it may be a bit hard for you to grasp its significance. To help your understanding, I will supply a few illustrations.

First, the picture of a Newtonian motion in a familiar space-time diagram (space is reduced to two dimensional, for obvious reasons):

Barbour is going to propose an alternative way, in terms of a timeless frame. Confined to this simple example, it is Triangle Land, a 3-dimensional Platonia.

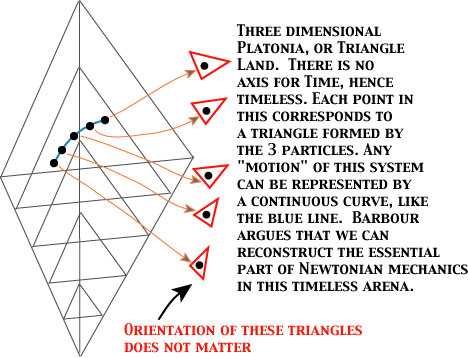
But, of course, we have powerful experiences of "time" in our everyday life and in physics. So the crucial question is: how can we recover (or explain) these experiences of "time"? Barbour's answer, in a word, is: if we can reconstruct mechanics (the essential part of the Newtonian mechanics, with this instance) in this timeless frame, time can be reconstructed as a "derivable structure" from this mechanics. Not "space and time first, then mechanics", but "mechanics first, then time" (space, Euclidean 3 space, is presupposed at this stage).

Then comes a harder part on quantum mechanics and quantum cosmology. As Barbour briefly suggests, he is sympathetic with Wheeler-DeWitt equation and Hawking's development of this line. But what is Wheeler-DeWitt equation supposed to mean? As is well known, the global or macroscopic structure of the universe can be described by general relativity, but when it comes to tiny things, atoms, elementary particles, or black holes for that matter (it is supposed to shrink to zero volume, according to general relativity), you cannot neglect quantum effect. Now the "big bang" cosmology tells us that the universe began from a tiny state, to which quantum mechanics certainly applies. Then the wave function of quantum mechanics must hold for the whole (and beginning) universe, and an equation for this is Wheeler-DeWitt equation; there can be various (possible) states of the universe, and this equation can determine the probability of each state (you've got to solve the equation, usually with an initial and boundary condition). As Barbour sees, this probability distribution must be made in timeless manner; hence the idea fits Barbour's idea of Platonia (relative configuration space). Hawking comes in because he proposed "no boundary condition" for the universe (see this); and this nicely leads to the "inflation" theory of big bang ("inflation" means an accelerated expansion at the early stage). Thus, the upshot is that if we wish to get into quantum gravity and quantum cosmology, we've got to consider a probability distribution over possible states of the universe (or possible universes, for short).

Barbour's talk on the "number of the same triangle in the bag" (Barbour, 36), and later, on "a mist in Platonia" (51) is meant for covering the preceeding circumstances. When we begin to consider quantum effect, we cannot identify any unique path in Platonia, only probabilities over possible paths. Many people may find this idea hard to accept. But there is an alternative called "many-world interpretation" of quantum mechanics, and thus the question of space and time merges with the question of interpretation of quantum mechanics.

Reference

Davies, P.C.W., and Brown, J.R., eds., The Ghost in the Atom, Cambridge University Press, 1986（『量子と混沌』出口修至訳、地人書館、1987）[For various interpretations of quantum mechanics]