

Rods and Clocks in Motion
Section Twelve
The results of the Lorentz transformation can be applied to the measuring-rods and clocks in two coordinate systems in relative motion. Here is a figure summarizing the results.
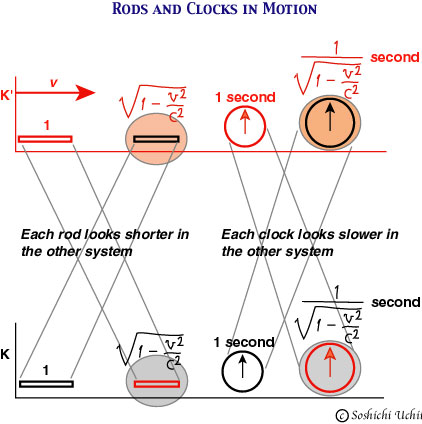
In a word, if K' moves with velocity v relative to K, the rod looks shorter (spatial contraction) to the observer in K (along the direction of the motion), and the clock looks slower (time delay). However, there is a definite relationship between the two quantities in the two systems, and there is no difficulty for doing physics with this "relativity".
These results may seem tedious; but if we introduce the Minkowski (4 dimensinal) space (Section 17), everything becomes simpler. For example, the change of time in two systems can be represented by the following figure (which takes time and only one dimension of space), if we may use Minkowski space (if you do not understand at this stage, do not worry).
Notice that (1) any horizontal line in K expresses the relation of simultaneity, and that (2) the clock in K' records time along its time axis (red, in the figure); seen from K, the unit of time °„in K' becomes t (more of this later). Do not say t is smaller than °„; in Minkowski space, Geometry looks similar to Euclidean geometry, but it is actually different. We have
tt = °„°„+ ss,
so that t is actually larger than °„! (Notice that this new geometry takes time into consideration, in addition to space; which may be called the Lorentz geometry.) If you wish to represent the state of affairs from K', K has the reversed velocity relative to K', so all you need to do is to take the mirror image of the preceding figure (with respect to the vertical axis), and rename the black and red axes, and the same relation holds.
Thus, although Einstein introduced new ideas of space and time in his special relativity, he still did not have a good way to express these ideas.
Last modified, April 23, 2002. (c) Soshichi Uchii
suchii@bun.kyoto-u.ac.jp