

Coordinate Transformation, from Acceleration to Gravity
Let's continue our consideration of a uniformly accelerated system. We can construct a coordinate system for the accelerated observer, in the following manner, starting from the original Lorentz system. It may look like this, as Zhukov nicely depicted:
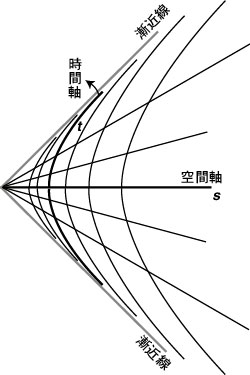
Thick lines are the spatial axis and the time axis, and notice that the time axis is curved (hyperbola); so this is already a curved coordinate system. And as we have already seen, from the consideration of this system we can reach the law of gravitational fields, at least approximately. But the observer on the time axis may want to represent his/her axis as a straight line (for, as Einstein says many times, the observer has a right to regard himself/herself as at rest); the preceding system is inconvenient in that the spacetime outside of the two asymptotes cannot be represented. So let us make the time axis straight! This can be done by a coordinate transformation; but the important thing is to keep the law of gravity intact by this transformation. How should we do this? Here is a schematic answer.
The law of gravity in the rightmost system is physically equivalent with the law (of inertial motion) in the leftmost system. Of course, you have to match the change of metric with the coordinate transformation, in order to keep the law intact; but you can intuitively understand that this can be done. Thus you can have a glimpse of what is called the "general covariance".
Reference
ランダウ+ジューコフ『相対性理論入門』(鳥居・広重・金光訳)東京図書、1977 (see pp. 158, 188-192)。
Last modified, July 12, 2003. (c) Soshichi Uchii
suchii@bun.kyoto-u.ac.jp