![]()
![]()
![]()
![]()
Galton's Quincunx
ª@its use to provide an analogue proof that a normal mixture of normal distributions was itself normal was a stroke of genius. . . . The crucial point is that Galton's conceptual use of the result was new and ingenious and represents the most important step in perhaps the single major breakthrough in satstics in the last half of the nineteenth century. This concept freed Galton of the restrictions of naive error theory without requiring that he go beyond that theory. He could conceive of his data as a mixture of very different populations, notwithstanding the unity apparent in its normal outline. (Stigler 1986, 281)
ª@
In order to apply the "law of error" to statistical analysis of heredity, Galton devised a tool called "quincunx" (around 1873 or 1874). By this means, he could show that normal distribution is normally a mixture of normal distributions. The following figure is Karl Pearson's drawing based on Galton's original sketches. In the middle row, figure II shows the two-stage quincunx.
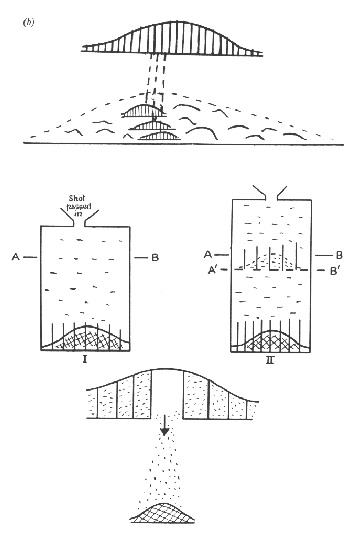
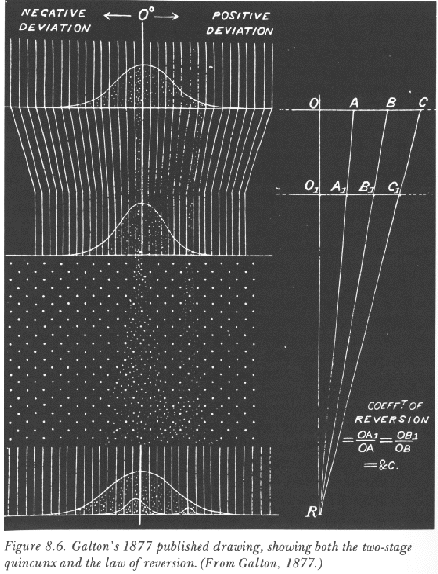
The following figure is that which Galton used in his 1877 paper (on sweet peas). You can see a regular pattern of five pins, and hence the name "quincunx". The upper part shows how two distributions with different "width" (or dispersion) are related; and the lower part shows the two-stage quncunx. On the right-hand side, the law of reversion (see below) is illustrated. (Figures from Stigler 1986)
ª@
Let us quote Kevles's passage:
Galton's interest ... was not in the mean but in the distribution of deviations from it. . . . he came independently to view the Gaussian distribution not primarily as a way of differentiating true values from false ones but as a tool for analyzing populations in terms of their members' variations from a mean---the kind of variations inevitably manifest in, for example, the heights or weights of a large, randomly selected group of people. Eventually, he concluded that there was "scarecely anything so apt to impress the imaginationas the wonderful form of cosmic order expressed by the 'Law of Frequency of Error,' . . . (Kevles 1985, 13-4)
Thus it should be kept in mind that Galton wanted to apply his findings by means of quincunx to human heredity. One step toward this goal was accomplished by Galton's study on sweet peas (Kevles 1985, 14-5). Stigler's (rather than Kevles's) summary is quite useful.
In 1875 Galton had arranged for several friends to assist him by growing sweet peas from packets of seeds that Galton had carefully separated by weight into seven groups .... By 1877, ..., he had completed an analysis of these data, the produce of 7 sizes ª~10 seeds per size ª~7 friends = 490 seeds, with surprising findings. ...
Galton found that if he looked separately at the seven groups of progeny seeds, groups classified by weight of parent seed from heaviest ... to lightest ..., each group separately followed a normal curve and, in addition, the curves, although centered at different weights, were equally disperse. ... The groups of seeds had behaved just like the shot from the different compartments at the AB level of the quincunx [see the last Figure 8.6 above]. Each had produced a little normal curve (as in Figure 8.6), and the curves were equally disperse. ...
But how could one account for the seeds' stability? Why did the dispersion among the progeny seeds not lead to populations that were increasingly variable from generation to generation? Galton's answer---his second major finding---was reversion. The seven groups of progeny were normally distributed, but not about their parents' weight. Rather they were in every case distributed about a value that was closer to the average population weight than was that of the parent. Furthermore, this reversion followed "the simplest possible law"; that is, it was linear. The average deviation of the progeny from the population aveag a same direction as that of the parent, but only a third as great. The mean progeny reverted to type, and the increased variation was just sufficient to maintain the population variability. (Stigler 1986, 281-2)
However, Galton still had a long way to go to human heredity. He conducted a study on human heights in 1885.
Last modified October 26. (c) Soshichi Uchii