

Leibniz-Clarke Correspondence, Part 2
G. W. Leibniz (1646-1716); Samuel Clarke (1675-1729)
Leibniz now tries to expound his view in more detail in his 5th Paper; so that, for a while, Leibniz continues his monologue. But I will add a brief note on Clarke's response, when necessary. All quotations are from Alexander, ed., Leibniz-Clarke Correspondence, Manchester University Press, 1956.
The Identity of Indiscernibles, Moveability of the finite
27. The parts of time or place, considered in themselves, are ideal things: and therefore they perfectly resemble one another like two abstract units. But it is not so with two concrete ones, or with two real times, or two spaces filled up, that is, truly actual.
28. I don't say that two points of space are one and the same point, nor that two instants of time are one and the same instant, as the author seems to charge me with saying. But a man may fancy, for want of knowledge, that there are two different instants, where there is but one: in like manner as I observged in the 17th paragraph of the foregoing answer, that frequently in geometry we suppose two, in order to represent the error of a gainsayer, when there is really but one. If any man should suppose that a right line cuts another in two points; it will be found after all, that those two pretended points must coincide, and make but one point.
29. I have demonstrated, that space is nothing else but an order of the existence of things, observed as existing together; and therfore the fiction of a material finite universe, moving forward in an infinite emty space, cannot be admitted. It is altogether unreasonable and impracticable. For, besides that there is no real space out of the material universe; such an action would be without any design in it: it would be working without doing any thing, agendo nihil agere. There would happen no change, which could be observed by any person whatsoever. These are imaginations of philosophers who have incomplete notions, who make space an absolute reality. Mere mathematicians, who are only taken up with the conceits of imagination, are apt to forge such notions; but they are destroyed by superior reasons.
31. I don't grant, that every finite is moveable. According to the hypothesis of my adversaries themselves, a part of space, though finite, is not moveable. What is moveable, must be capable of changing its situation with respect to something else, and to be in a new state discernible from the first: otherwise the change is but a fiction. A moveable finite, must therefore make part of another finite, that any change may happen which can be observed. (Leibniz's 5th Paper, Alexander 1956, 63-4)
Uchii's Note: Leibniz tries to elucidate his distinction between "ideal" and "actual" things; and he restricts the applicability of the principle of the identity of indiscernibles to the latter. And he rejects Clarke's alleged "conclusive proof" from the moveability of finite things. Against this, Clarke now explicitly appeals to the case of circular motion and centrifugal force (Clarke's 5th Reply, Alexander 1956, 101), and he rightly complains that Leibniz neglected this.
Empty Space
33. Since space in itself is an ideal thing, like time; space out of the world must needs be imaginary, as the schoolmen themselves have acknowledged. The case is the same with empty space within the world; which I take also to be imaginary, for the reason before alleged.
34. The author objects against me the vacuum discovered by Nr. Guerike of Madenburg, which is made by pumping the air out of a receiver; and he pretends that there is truly a perfcect vacuum, or a space without matter, (at least in part,) in that receiver. The Aristotelians and Cartesians, who do not admit a true vacuum, have said in answer to that experiment of Mr. Guerike, as well as to that of Torricellius of Florence, (who emptied the air out of a glass-tube by the help of quicksilver,) that there is no vaccum at all in the tube or in the receiver; since glass has small pores, which the beams of light, the effluvia of the load-stone, and other very thin fluids may go through. I am their opinion: (Leibniz's 5th Paper, Alexander 1956, 64-5)
Uchii's Note: Leibniz then touches on the question of vacuum; although it may seem to the modern reader that Leibniz is clearly wrong here, it must be remembered that there are two longstanding tranditions as regards vacuum, and the "ether" supposed (for electro-magnetism) in the 19th century was a kind of matter. And although Einstein's relativity theory is generally regarded as enabling us to discard "ether", the new vacuum now supports "fields" for electro-magnetism and gravity (fields are "substantive" to the modern substantivalist, whereas the modern relationist has a great difficulty for reconstructing fields as "relations"!).
What is Place, What is Space?
47. I will here show, how men come to form to themselves the notion of space. They consider that many things exist at once and they observe in them a certain order of co-existence, according to which the relation of one thing to another is more or less simple. This order, is their situation or distance. When it happens that one of those co-existent things changes its relation to a multitude of others, which do not change their relation among themselves; and that another thing, newly come, acquires the same relation to the others, as the former had; we then say, it is come into the place of the former; and this change, we call a motion in that body, where in is the immediate cause of the change. And though many, or even all the co-existent things, should change according to certain known rules of direction and swiftness; yet one may always determine the relation of situation, which every co-existent acquires with respect every other co-existent; and even that relation which any other co-existent would have to this, or which this would have to any other, if it had not changed, or if it had changed any otherwise. And supposingl or feigning, that among those co-existents, there is a sufficient number of them, which have undergone no change; then we may say, that those which have such a relation to those fixed existents, as others had to them before, have now the same place which those others had. And that which comprehends all those places, is called space. Which shows, that in order to have an idea of place, and consequently of space, it is sufficient to consider these relations, and the rules of their changes, without needing to fancy any absolute reality out of the things whose situation we consider. And, to give a kind of a defnition: place is that, which we say is the same to A and, to B, when the relation of the co-existence of B, with C, E, F, G etc. agrees perfectly with the relation of the co-existence, which A had with the same C, E, F, G, etc. It may be said also, without entering into any further particularity, that place is that, which is the same in different moments to different existent things, when their relations of co-existence with certain other existents, which are supposed to continue fixed from one of those moments to the other, agree entirely together. And fixed existents are those, in which there has been no cause of any change of the order of their co-existence with others; or (which is the same thing,) in which there has been no motion. Lastly, space is that, which results from places taken together. (Leibniz's 5th Paper, Alexander 1956, 69-70)
Uchii's Note: Here Leibniz's definitions are over, and he adds some explanations and analogous examples. But let me insert an illustration of what Leibniz is saying on place and space.
Leibniz Space 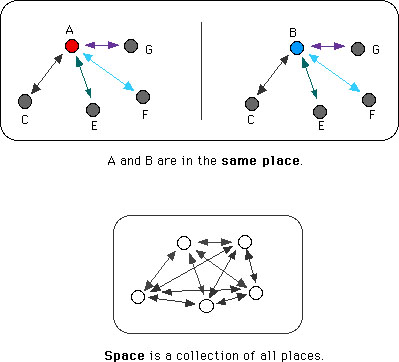
As regards the last figure (bottom), it may be hard for you to grasp its significance. But one thing is clear: it shows one of the possible configurations among the objects. And it is certainly a viable choice to pursue a theory of space and time, and of physics, in terms of such configurations as a basic element. For a contemporary attempt, see The End of Time, or the Beginning of the New Machianism?.
Ideality of Place and Space
 And
here it may not be amiss to consider the difference between place, and the relation
of situation, which is in the body that fills up the place. For, the place of
A and B, is the same; whereas the relation of A to fixed bodies, is not precisely
and individually the same, as the relation which B (that comes into its place)
will have to the same fixed bodies; but these relations agree only. For, two
different subjects, as A and B, cannot have precisely the same individual affection;
it being impossible, that the same individual accident should be in two subjects,
or pass from one subject to another. But the mind not contented with an agreement,
looks for an identity, for something that should be truly the same and conceives
it as being extrinsic to the subjects: and this is what we call place
and space. But this can only be an ideal thing; containing a certain
order, wherein the mind conceives the application of relations.
And
here it may not be amiss to consider the difference between place, and the relation
of situation, which is in the body that fills up the place. For, the place of
A and B, is the same; whereas the relation of A to fixed bodies, is not precisely
and individually the same, as the relation which B (that comes into its place)
will have to the same fixed bodies; but these relations agree only. For, two
different subjects, as A and B, cannot have precisely the same individual affection;
it being impossible, that the same individual accident should be in two subjects,
or pass from one subject to another. But the mind not contented with an agreement,
looks for an identity, for something that should be truly the same and conceives
it as being extrinsic to the subjects: and this is what we call place
and space. But this can only be an ideal thing; containing a certain
order, wherein the mind conceives the application of relations.
In like manner, as the mind can fancy to itself an order made up of genealogical lines, whose bigness would consist only in the number of generations, wherein every person would have his place: and if to this one should add the fiction of a metempsychosis, and being in the same human souls again; the persons in those lines might change place; he who was a father, or a grandfather, might become a son, or a grandson, etc. And yet those genealogical places, lines, and spaces, though they should express real truth, would only be ideal things.
I shall allege another example, to show how the mind uses, upon occasion of accidents which are in subjects, to fancy to itself something answerable to those accidents, out of the subjects. The ratio or proportion between two lines L and M, may be conceived three several ways; as a ratio of the greater L, to the lesser M; as a ratio of the lesser M, to the greater L; and lastly, as something abstracted from both, that is, as the ratio between L and M, without considering which is the antecedent, or which the consequent; which the subject, and which the object. And thus it is, that proportions are considered in music. In the first way of considering them, L the greater; in the second, M the lesser, is the subject of that accident, which philosophers call relation. But, which of them will be the subject, in the third way of considering them? It cannot be said that both of them, L and M together, are the subject of such an accident; for if so, we should have an accident in two subjects, with one leg in one, and the other in the other; which is contrary to the notion of accidents. Therefore we must say, that this relation, in this third way of considering it, is indeed out of the subjects; but being neither a substance, nor an accident, it must be a mere ideal thing, the consideration of which is nevertheless useful.
To conclude: I have here done much like Euclid, who not being able to make his readers well understand what ratio is absolutely in the sense of geometricians; defines what are the same ratios. Thus, in like manner, in order to explain what place is, I have been content to define what is the same place. Lastly; I observe, that the traces of moveable bodies, which they leave sometimes upon the immoveable ones on which they are moved; have given men occasion to form in their imagination such an idea, as if some trace did still remain, even when there is nothing unmoved. But this is a mere ideal thing, and imports only, that if there was any unmoved thing there, the trace might be marked out upon it. And 'tis this analogy, which makes men fancy places, traces and spaces; though those things consist only in the truth of relations, and not at all in any absolute reality. (Leibniz's 5th Paper, Alexander 1956, 70-2; The original long paragraph is divided into several, by Uchii.)
Uchii's Note: Maybe Leibniz's discussion here is confusing to the modern reader; but notice that Leibniz is still considering in terms of the subject-predicate form of a proposition ("logic of relations" comes in the 19th century!). (1) So he has some difficulty for handling relations; and this difficulty tends to be mixed up with the question of "ideality". (2) But according to the modern logic, monadic predicates (for a property or "accident" as Leibniz put it) are on a par with dyadic predicates (for relations); does this show Leibniz's argument is meaningless? No, because he would regard the construction of an ordered pair (for talking about a relation in set-theoretical terms) as a sort of "ideal" operation. (3) His analogies with genealogical relations and with ratio may not be quite right, but they may help to grasp the meaning of his denial of "reality" to space. Anyway, he is after the criterion for identity of place; a similar problem (individuation of physical space-time points) appears, according to John Stachel, in general relativity (see the last section of my Genesis of General Relativity 6). Unfortunately, Clarke seems to have neglected , intentionally or unintentionally, to pay attention to this important paragraph (Alexander 1956, 104).
Don't confuse things persisting in time with time itself
49. It cannot be said that [a certain] duration is eternal but [it can be said] that the things which continue always are eternal, [gaining always a new duration.] Whatever exists of time and of duration, [being successive] perishes continually: and how can a thing exist eternally, which (to speak exactly,) does never exist at all? For, how a thing can exist, whereof no part does ever exist? Nothing of time does ever exist, but instants; and an instant is not even itself a part of time. Whoever considers these observations, will easily apprehend that time can only be an ideal thing. And the analogy between time and space, will easily make it appear, that the one is as merely ideal as the other. [But, if in saying that the duration of a thing is eternal, it is only meant that the thing endures eternally, I have nothing to say against it.] (Leibniz's 5th Paper, Alexander 1956, 72-3)
Uchii's Note: Leibniz here warns against a sort of "category mistake", as regards statements about time. But Clarke responds, "These seem to me, to be only a quibbling upon words"; thus he seems to be determined to refuse to listen to what Leibniz is trying to say (Alexander 1956, 104).
Observability, Rotation, and Quantity
52. In order to prove that space, without bodies, is an absolute reality; the author objected, that a finite material universe might move forward in space. I answered, it does not appear reasonable that the mateiral universe should be finite; and, though we should suppose it to be finite; yet 'tis unreasonable it should have motion any otherwise, than as its parts change their situation among themselves; because such a motion would produce no change that could be observed, and would be without design. 'Tis another thing, when its parts change their situation among themselves; for then there is a motion in space; but it consists in the order of relations which are changed. The author replies now, that the reality of motion does not depend upon being observed; and that a ship may go forward, and yet a man, who is in the ship may not perceive it. I answer, motion does not indeed depend upon being observed; but it does depend upon being possible to be observed. There is no motion, when there is no change that can be observed. And when there is no change that can be observed, there is no change at all. The contrary opinion is grounded upon the supposition of a real absolute space, which I have demonstratively confuted by the principle of the want of a sufficient reason of things.
53. I find nothing in the Eighth Definition of the Mathematical Principles of Nature, nor in the Scholium belonging to it, that proved, or can prove, the reality of space in itself. However, I grant there is a difference between an absolute true motion of a body, and a mere relative change of its situation with respect to another body. For when the immediate cause of the change is in the body, that body is truly in motion; and then the situation of other bodies, with respect to it, will be changed consequently, though the cause of the change be not in them. 'Tis true that, exactly speaking, there is not any one body, that is perfectly and entirely at rest; but we frame an abstract notion of rest, by considering the thing mathematically. Thus have I left nothing unanswered, of what has been alleged for the absolute reality of space. And I have demonstrated the falsehood of that reality, by a fundamental principle, one of the most certain both in reason and experience; against which, no exception or instance can be alleged. Upon the whole, one may judge from what has been said that I ought not to admit a moveable universe; nor any place out of the material universe.
54. I am not sensible of any objection, but what I think I have sufficiently answered. As for the objection that space and time are quantities, or rather things endowed with quantity; and that situation and order are not so: I answer, that order also has its quantity; there is in it, that which goes before, and that which follows; there is distance or interval. Relative things have their quantity, as well as absolute ones. For instance, ratios or proportions in mathematics, have their quantity, and are measured by logarithms; and yet they are relations. And therefore though time and space consist in relations, yet they have their quantity. (Leibniz's 5th Paper, Alexander 1956, 73-5)
Uchii's Note: In 52, Leibniz clarifies his assertion of the dependence of motion as "dependence on being possible to be observed". In 53, Leibniz admits the distinction between absolute and relative motion; but he does not address himself to the problem of rotation (Newton's bucket-experiment). Finally, in 54 he refers to the problem of quantity, but his answer is merely sketchy, to say the least, and does not say "how quantities can be incorporated into relationalism". Thus Clarke's complaint (5th Reply 54, Alexander 1956, 105) is justifiable.
How Clarke misunderstood Leibniz's view on time
55. As to the question, whether God could have created the world sooner; 'tis necessary here to understand each other rightly. Since I have demonstrated, that time, without things, is nothing else but a mere ideal possibility; 'tis manifest, if any one should say that this same world, which has been actually created, might have been createed sooner, without any other change; he would say nothing that is intelligible. For there is no mark or difference, whereby it would be possible to know, that this world was created sooner. And therefore, (as I have already said,) to suppose that God created the same world sooner, is supposing a chimerical thing. 'Tis making time a thing absolute, independent upon God; whereas time does only co-exist with creatures, and is only conceived by the order and quantity of their changes.
56. But yet, absolutely speaking, one may conceive that an universe began sooner, than it actually did. Le us suppose our universe, or any other, to be represented by the Figure AF; and that the ordinate AB represents its first state; and the ordinates CD, EF, its following states: I say, one may conceive that such a world began sooner, by conceiving the figure prolonged backwards, and by adding to it SRABS. For thus, things being increased, time will be also increased. But whether such an augmentation be reasonable and agreeable to God's wisdom, is another question, to which we answer in the negative; otherwise God would have made such an augmentation. ... The case is the same with respect to the destruction of the universe. As one might conceive something added to the beginning, so one might also conceive something taken off towards the end. But such a retrenching from it, would be also unreasonable.
57. Thus it appears how we are to understand, that God created things at what time he pleased; for this depends upon the things which he resolved to create. But things being once resolved upon, together with their relations; there remains no longer any choice about the time and the place, which of themselves have nothing in them real, nothing that can distinguish them, nothing that is at all discernible.
58. One cannot therefore say, as the author does here, that the wisdom of God may have good reasons to create this world at such or such a particular time: that particular time, considered without the things, being an impossible fiction; and good reasons for a choice, being not to be found, where everything is indiscernible. (Leibniz's 5th Paper, Alexander 1956, 75-7)
Uchii's Note: Here, Leibniz takes pains with pointing out Clarke's misunderstanding in his objection. Since time depends on the things ordered, it does not make sense for Leibniz to talk about time before creation. You can conceive another creation (by God), but the time of that world is different from the time of our world; and there must be a sufficient reason for God for choosing either. However, Clarke again refuses to try to understand: he says "All this, seems to me to be a plain contradiction" (Alexander 1956, 107). This sort of obstinacy is disgraceful; if you allege too many contradictions in a respectable writer, it is you who is to be blamed!
Matter and Space, different but inseparable
62. I don't say that matter and space are the same thing. I only say, there is no space, where there is no matter; and that space in itself is not an absolute reality. Space and matter differ, as time and motion. However, these things, though different, are inseparable.
Uchii's Note: Since Clarke said, in paragraph 15 of his 4th reply, "they who suppose matter and space to be the same", Leibniz added this comment.
How does God place two equal cubes in different places?
67. The parts of space are not determined and distinguished, but by the things which are in it: and the diversity of things in space, determines God to act differently upon different parts of space. But space without things, has nothing whereby it may be distinguished; and indeed not any thing actual.
68. If God is resolved to place a certain cube of matter at all, he is also resolved in what particular place to put it. But 'tis with respect to other parts of matter; and not with respect to bare space itself, in which there is nothing to distinguish it. (Leibniz's 5th Paper, Alexander 1956, 78-9)
Uchii's Note: In response to Clarke's example of two equal cubes placed consecutively. Leibniz is saying, "Don't say there are two similar places in advance in space, and God considers how to place two equal cubes; by deciding, at once, how to place the two, He creates both the cubes and their places."
Order of situations, order and quantity
104. I don't say, that space is an order or situation, which makes things capable of being situated: this would be nonsense. Any one needs only consider my own words, and add them to what I said above, (Numb. 47) in order to show how the mind comes to form to itself an idea of space, and yet that there need not be any real and absolute being answering to that idea, distinct from the mind, and from all relations. I don't say therefore, that space is an order or situation, but an order of situations; or (an order) according to which, situations are disposed; and that abstract space is that order of situations, when they are conceived as being possible. Space is therefore something [merely] ideal. But, it seems, the author will not understand me. I have already, in this paper, (Numb. 54,) answered the objection, that order is not capable of quantity.
105. The author objects here, that time cannot be an order of successive things, because the quantity of time may become greater or less, and yet the order of successions continue the same. I answer; this is not so. For if the time is greater, there will be more successive and like states interposed; and if it be less, there will be fewer; seeing there is no vacuum, nor condensation, or penetration, (if I may so speak), in times, any more than in places. (Leibniz's 5th Paper, Alexander 1956, 89-90)
Uchii's Note: Clarke misunderstood Leibniz by giving a wrong paraphrasing. Leibniz's answer as regards the quantity of time is not satisfactory, as was already pointed out above; however, we have to wait for Riemann in order to get a clue to the question of quantity with respect to space and time. [Since Clarke's 5th Reply is too unpleasant and disgraceful, I will not continue any further. Aho-to-chauka?]
back to Part 1
Last modified June 25, 2004.(c) Soshichi Uchii suchii@bun.kyoto-u.ac.jp