

The Principle of Extremal Aging, and Momenergy
The Principle of Extremal (Maximal) Aging
In order to bridge the gap between special relativity and general relativity, we have to know the Principle of Extremal Aging (Taylor & Wheeler 1992, 150; Taylor & Wheeler 2000, 1-7).
The path a free particle takes between two events in spacetime is the path for which the time lapse between these events, measured by the clock on the particle, is an extremum (maximum).
Let us begin with a movement of a free particle in special relativity. As you already know, its trajectory is a straight line in the Minkowski space; so let us represent it by a vertical line in the following figure; and let us imagine, for the sake of comparirson, any curve deviating from this straight line but coinciding with it at the starting point and the end point.
The total time along this curve (from "Start" and to "End") is a sum of the proper time along this curve. So take any small segment (d°„) of this curve; then according to the Lorentz metric,
(d°„)(d°„) = (dt)(dt) ª|(ds)(ds)
It is easy to see that d°„ is at most equal, and generally smaller than, dt; thus unless the curve completely agrees with the straight path, the proper time from "Start" to "End" is smaller than the proper time along the straight path. Thus we have obtained a version of the principle of extremal aging, in special relativity. We took a vertical line, but this does not diminish the generality, because the argument can easily be adapted to any straight (timelike) line. And it turns out that the principle holds even in a curved spacetime; it determines the path of a free particle, so to speak, and the path is nothing but a geodesic, a longest path between two events (in many books and articles, a geodesic is said to be a shortest path; this is true on a spatial surface such as a sphere, but notice that we are dealing with the Lorentzian geometry of spacetime).
In terms of this principle, we can easily answer the so-called "Twin Paradox": Alice and Betty are a twin, and Alice stays home (the blue worldline, in the preceding figure) while Betty takes a spaceship, goes out of the earth and returns some years later (the red worldline); on her return, which is older, Alice or Betty? Despite the fact that their relative motion seems identical, Alice stays on a straight path in spacetime and Betty takes a curved path. Thus according to the principle of extremal aging, it is Alice who became older. We can say this because of the preceding Lorentz metric, not necessarily from geometrical images of "straight" or "curved".
Here is a specific example in terms of a simplified combination of two straight motions: Alice stays on the Earth (which is assumed to be an inertial system) and Betty takes a round trip to the Star S, at a distance of 10 light-years from the Earth, on a spaceship with the velocity of one half of that of light; we disregard the time for acceleration, for changing the direction of the motion.
With this example, you can calculate according to the Lorentz metric (no need for integration, because Betty's path is straight, both for going and coming back). Now which is older, when Alice and Betty meet again on Betty's return? 40 years pass for Alice on the Earth; whereas for Betty, 17.3 years for going and 17.3 years for returning, and 34.6 years for the entire trip. Thus Betty is younger when they meet again. Notice that the surface of simultaneity for Betty radically changes, before and after she changes her direction.
Although the principle of extremal aging may seem trivial, it is essential for defining an essential feature of mass in motion, momentum-energy, or momenergy (according to Wheeler's terminology). According to the Newtonian mechanics, momentum is mv (massª~velocity) and kinetic energy is (1/2)mvv; however, in special relativity, three things are unified, and we have a single quantity, momenergy. Henceforth, we assume both energy and momentum are expressed in units of mass.
Momenergy or Momentum-Energy
To be more specific, from the metric and the principle of extremal aging, we can derive two constants of the motion for a free particle. One is the energy per unit mass,
E/m = dt/d°„
and another is the momentum per unit mass,
p/m = ds/d°„
where ds is a small spatial displacement during the motion. These can be beautifully represented in a geometrical figure (adapted from Taylor & Wheeler 1992, Figure 7-1).
As you can see in this picture, at any event in spacetime, the momenergy of a particle in motion points in the same direction as its worldline; energy is its "time-part", and momentum, its "space-part". As a special case, see the momenergy of light ray; since the proper time on light ray is zero, momenergy is also zero, or in other words, momentum and energy are equal and cancel out. And what's important is that the law of conservation of momenergy holds: the total momenergy of an isolated system (of particles) is conserved. Further, since in the preceding figure the momenergy is shown as a unit vector (per unit mass), the mass m of the particle may be regarded as the magnitude of the whole vector attached to the particle.
As a consequence of all this, it should be clear that momentum and energy are relative, i.e. different for different observers, but momenergy and mass (determined by momentum and energy) are invariant, independent of the reference frame. [This exposition owes a great deal to Taylor & Wheeler 1992, ch. 7, and Taylor & Wheeler 2000, 1-7 to 1-13.]
For your convenience, I will add two more figures of momenergy, one for 3 dimensional case, and the other for 4 dimensional case (somehow deformed for an easier view).
We dwell on momenergy, because this is one of the essential ingredients of Einstein's field equations: on the left, the curvature (tensor), on the right, the momentum-energy (tensor), and the two grip each other. And the interaction between spacetime and mass takes place in the boundaries (faces of a cube) of a boundary (each 3-dimensional cube, surrounding a block of 4-dimensional spacetime); see Figure, which is adapted from Wheeler (1999), 112, and Misner, Thorne, and Wheeler (1973), 366. If you feel some difficulty, read t, before-after; x, west-east; y, south-north; z, down-up. Since each axis has two directions, we have 2 times 4 axes, i.e., 8 cubes; a slice of 4-dimensional spacetime is 3-dimensional, you may recall. This way, we can visualize a 4-dimensional cube, so to speak. If you look at this 4-cube from bottom to top, you may notice two layers of time. The bottom hexagon (its lower part is labelled by z_1, t_1, and x_2) is at t_1; and the top hexagon (its upper part is labelled by x_1, t_2, and z_2) is at t_2. Likewise you can find hexagons at x_1, x_2, y_1, etc., by changing your perspective.
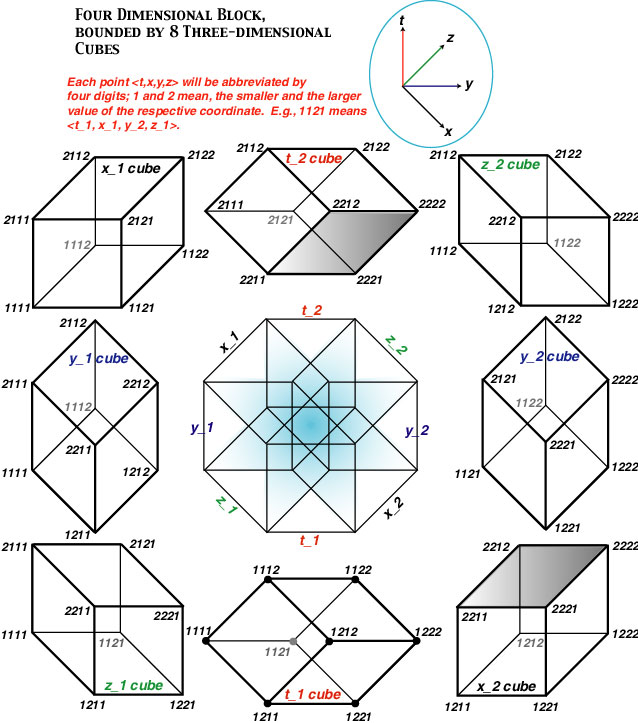
Have you noticed that, if you fix the time (e.g., t_1), you obtain a particular cube (center, bottom), and if you fix the spatial point (e.g., z_1), you obtain another cube (left, bottom)? Also, notice that every face of every 3-dimensional cube (e.g., <2211, 2212, 2222, 2221>) is counted twice, once in one cube (center, top), and once in another cube (right, bottom); these two cubes share the same face, and each is out of the other (the two cubes are on the opposite sides of the face; technically, the face is counted twice, with the opposite orientation). In this 4-dimensional block, the total momenergy is conserved; and the momenergy in each 3-dimensional cube, acting on each face, determines its curvature. More on this later (if you want to study in advance, see Misner, Thorne, and Wheeler 1973, ch. 15, and Wheeler 1999, ch. 7).
References
Misner, Thorne, and Wheeler (1973) Gravitation.
Taylor & Wheeler (1992) Spacetime Physics, 2nd ed., Freeman, 1992.
Taylor & Wheeler (2000) Exploring Black Holes, Addison, Wesley, Longman, 2000.
Wheeler, J. A. (1999) A Journey into Gravity and Spacetime, Scientific American Library, 1999.
Last modified August 30, 2002.(c) Soshichi Uchii suchii@bun.kyoto-u.ac.jp