

The Parable of the Apple
The Parable of the Apple
We now have a number of popular expositions of the theory of general relativity, including Einstein's own version (1917) and such classics as Eddington's Space, Time and Gravitation (1920) and Geroch's General Relativity from A to B (1978). But to my knowledge (not extensive, I warn you!), Misner, Thorne and Wheeler's "Parable of the Apple" in Chapter 1 of their Gravitation (1973) is the best, in that it gives a basic and overall view and the analogy used goes far enough, giving clear hints on the nature of mathematical tools used in the theory. The book itself is as thick as a phone-directory book, but it is quite useful for beginners as well as for advanced students. Japanese scientists, if they complain about the "crisis of science education", should try to produce more textbooks on science as good as this (readable, intelligible, interesting, and yet rigorous) by their own hands and brains, I would say!
Wheeler, by the way, seems to be good at inventing a parable, since in his old textbook on special relativity (with E. F. Taylor, Spacetime Physics, 1963, also from Freeman and Co.), he used "Parable of the Surveyors" in order to illustrate the invariance of (Euclidean) distance.
The parable tries to explain the nature of gravitation in terms of the curvature of spacetime, and the two-dimensional curved surface (the curvature varies depending on locations) of the apple is used for this purpose. The following figure is adapted from their Figure 1.1.
The tale goes like this. One day a student, reflecting on the difference between Einstein's and Newton's views about gravity, noticed ants are running along the surface of an apple. Ants seemed to take a most economical path; wow, they are going along geodesics on this surface! But each geodesic may also be regarded as a path (world line) of a free particle on this surface (taken as a two-dimensional spacetime). Look at two ants going from the same spot on the top (near the dimple) into different directions; one goes down into the bottom of the dimple whereas the other goes around the dimple!
According to Newton, this is because of gravitation acting at a distance from a center of attraction. But according to Einstein, this is because of the local geometry of the surface at that spot, namely, because of the curvature of the spacetime there. But how do geometry and matter in the spacetime interact with each other? In brief, Einstein's geometrodynamics (according to his field equations) is "a double story of the effect of geometry on matter (causing originally divergent geodesics to cross) and the effect of matter on geometry (bending spacetime initiated by concentration of mass, symbolized by effect of stem nearby surface of apple)". Thus Einstein dispenses with any action-at-a-distance, and physics becomes simple only when analyzed locally. In a word, spacetime tells matter how to move, and matter tells spacetime how to curve (one of Wheeler's favorite phrases).
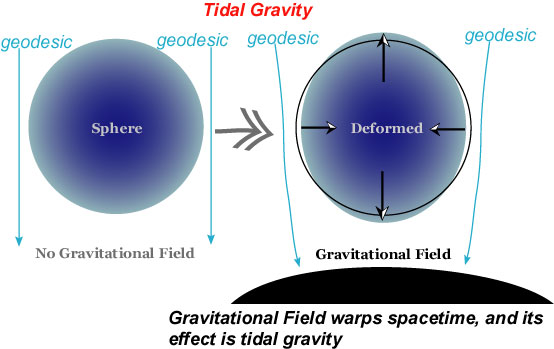
"How to move" part may be illustrated, aside from the above ant's paths, by the following figure, which shows tidal gravity, or tidal acceleration (as is well known, tide is caused by the gravity of the moon and the sun); this in general relativity, however, is explained in terms of geometry of spacetime. A free particle moves along a geodesic, and a body is deformed according to the local geometry.
"How to curve" part, on the other hand, may be illustrated by the spacetime warp produced by a star. The equatorial plane (N.B. this is a 2-space) crossing a star is not flat but warped (given an appropriate frame) because of the mass of the star, as is shown by the following embedding diagram (see Embedding Diagram), which visualizes the warp within an imaginary 3-space.
The matter of the star warps the plane in this manner; notice that on this plane the geometry is not Euclidean, since the circumference of the circle is smaller than diameter ü~ā╬. However, in order to obtain a deeper understanding of "how to curve" part, the notion of momentum-energy (usually expressed by stress-energy tensor) is indispensable. For this, see Wheeler's A Journey into Gravity and Spacetime, Scientific American Library, 1999, chh. 6-9.
Although the two parts together may seem circular, they are not; instead, these two parts make Einstein's field equation (see below) non-linear--not expressible in terms of a sum of parts or effects--so that it becomes very hard to obtain a solution for the equation.
It remains to add several supplementary remarks. Although the surface of the apple is curved, if you look at any local spot closely (by a magnifying glass), its geometry looks like that of a flat surface. Thus, a small region can be approximated by a local Lorentzian geometry which is familiar to you in terms of a Minkowski spacetime of the special relativity.
Next, you have got to realize that we can do physics without coordinates. For instance, "interval" in a Minkowski spacetime is an invariant quantity, not dependent on any coordinate system you choose, and likewise "curvature" can be treated independently from any coordinate system you may choose. We can treat physics both in coordinate-free language and coordinate-dependent language. For the coordinate-free language, vector (having a direction, like the separation between two events) plays an important role.
Further, you should forget about all the nice quantitative properties of the Euclidean space. Coordinates are one thing, and quantitative properties of physical events (expressed in them) are another thing. Important physical quantities in general relativity can be treated in terms of metric and curvature, closely associated with geometry. Metric is expressed by metric tensor g, which may be regarded as a machine with two input slots,
g(_, _)
inputs being a vector (with directions) associated with an event in spacetime; this gives (as its output) quantities necessary for determining the local geometry.
Curvature is more complicated. But the most important curvature, corresponding to the curvature of the surface of the apple, is expressed by the Riemann curvature tensor Riemann, which may be regarded as another machine with three inputs slots,
Riemann(_, _, _),
inputs again being a vector, and this machine gives (as its output) quantities necessary for calculating the path of any particle, like the path of an ant on the apple. Put in a nutshell, "geometry tells matter how to move" in this way.
The other direction ("matter tells spacetime how to curve") demands us to know the distribution of matter, which generates the stress-energy tensor T. In terms of the parable of the apple, what is the effect of stem in causing dimple? We have to know the distribution of matter around the stem, and that is expressed by T.
Now, a certain piece of the Riemann tensor, called the Einstein tensor is generated directly by the local distribution of matter; this tensor Einstein is "a sort of average of Riemann over all directions"; and Einstein's field equation relates Einstein and T in the following manner:
Einstein = 8ā╬T.
In a word, it shows how the stress-energy of matter generates an average curvature Einstein in its neighborhood. And this is a powerful equation governing all kinds of phenomena involving gravitation.
In order to fill in details of this basic outline, you have got to go through the main body of Misner, Thorne and Wheeler's thick volume, many times.
We now have good introductory books, such as the following, and these may be used together with Misner, Thorne, and Wheeler (1973):
Taylor, Edwin F. and Wheeler, J. A., Exploring Black Holes, Addison Wesley Longman, 2000.
Wheeler, J. A. (1999) A Journey into Gravity and Spacetime, Scientific American Library, 1999.
Last modified Sept. 2007. (c) Soshichi Uchii