

Derivation of the Lorentz Transformation
Appendix One
Einstein's derivation of the Lorentz transformation is not difficult, until he begins to discuss the propagation of a light signal. If you feel some difficulty, imagine the two-dimensional case where the signal propagates on the x-y surface, as in the following figure.
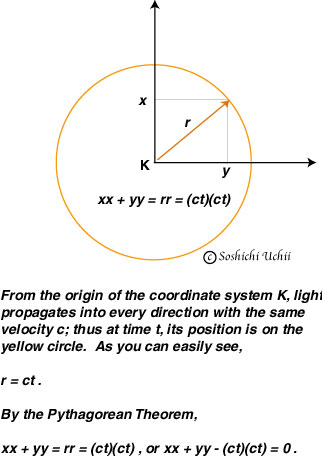
Since the light travels with the same velocity c into every direction, it depicts a circle of the radius r (i.e. ct), after time t. From this fact, it is easy to see that the square of the radius equals the sum of the square of x and the square of y. And if you generalize this to the three-dimensional case, you can understand Einstein's formula on page 136.
Incidentally, the relation
xx + yy = (ct)(ct) ,
together with the constancy of the velocity of light (in all inertial systems), is crucial for determining the Lorentz transformation, and hence the properties of Lorentz geometry characterized by it. In short, by treating time externally, and applying the Euclidean geometry to space, we obtained the essential relation for the Lorentz geometry, which treats time internally, on a par with spatial coordinates (time coordinate and spatial coordinates interact with each other, so to speak; and this aspect was very nicely captured by Minkowski space). In a technical word, the preceding relation is responsible for determining the Lorentzian metric, which completely determines the Lorentz geometry (you already know the Lorentzian metric; see the formula below the figure of Minkowski Space in Rods and Clocks).
Did anyone have this question: Is there any simpler (both mathematically and conceptually) derivation of the Lorentz transformation? Alan Macdonald offers "World's Fastest Derivation of the Lorentz Transformation"! He derives the Lorentz transformation, only in a page, from two assumptions: (A) The speed of light is the same in all inertial frames, and (B) a clock moving with constant velocity v, in an inertial frame, runs at a constant rate (presumably depending on v) with respect to the synchronized clocks (at rest in the same frame) which it passes. Notice that (B) follows from Einstein's relativity principle.
Last modified, May 14, 2002. (c) Soshichi Uchii
suchii@bun.kyoto-u.ac.jp