

Mechanics of Waves II
You may have had a trouble with Dr. Tomonaga's exposition of Planck Oscillator (a particle characterized by the motion of sinusoidal wave; Tomonaga 1969, 92, 144), and of Fourier Series, since Dr. Tomonaga assumes that the reader is familiar with the mathematical technique necessary for such expositions. If so, what you need is the understanding of the relationship between trigonometric functions and exponential functions via the complex numbers. This relationship is represented by Euler's Formula.
But, first, let us recall the simple sinusoidal wave.

Next, we have to recall elementary features of a complex number. A complex number is a number consisting of a real part and an imaginary part (having i such that i~i = -1):
a + ib
Now, any complex number can be represented geometrically, as in the following figure. 1 and i are incommensurable units, so to speak, in the plane containing all complex numbers.
This geometrical representation of complex numbers can introduce the relationship with trigonometric functions, since we can express the same thing both in terms of x-y coordinates and polar coordinates (r and Æ).
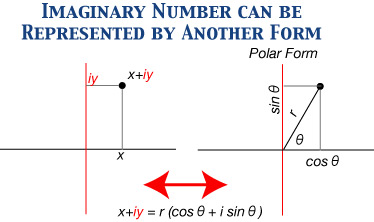
And it is usually convenient to use polar coordinates in order to express waves, because waves have a close relationship with trigonometric functions (as we have shown with sinusoidal waves).
Then, another concept comes in, that is, the exponential function. Maybe you know the special number e which appears in the natural logarithm. In mathematics of differentials and integrals, the exponential function with this e is most convenient, since the differential of e^x (xth power of e, and another expression is exp(x)) comes back to itself! You may have already noticed that this number plays a prominent role in statistical mechanics (see Tomonaga 1969, 259); but this is not the point here. Euler found a very important relation which connects this e, trigonometric function, and the complex number. The relation is called "Euler's Formula", and if you know this, you can understand many formulas in Dr. Tomonaga's book.
For instance, simply add the two exponential functions in the preceding figure, and you obtain a cosine function, 2cos Æ; thus a sinusoidal wave can be expressed in terms of exponential function (sine curve and cosine curve are essentially the same, and merely perspectives are different). Likewise, Fourier series, usually expressed in terms of trigonometric functions, can also be expressed in terms of exponential functions with complex numbers; this form is far more convenient for analytical treatment. For more on Euler's Formula, see Yoshida (1993).
Bohr, N. (1934), Atomic Theory and the Description of Nature, Ox Bow Press (reprint)
Tomonaga, S. (1969) ÊqÍw IiæQÅjAÝ·¸[B
Tomonaga, S. (1997) ÊqÍw IIiæQÅjAÝ·¸[B
Yoshida, T. (1993) IC[Ì¡¨ACÂÐB
See also a useful site on Microphysics, at Kyushu University: http://www2.kutl.kyushu-u.ac.jp/seminar/MicroWorld/MicroWorld.html