

Shells around the Nucleus
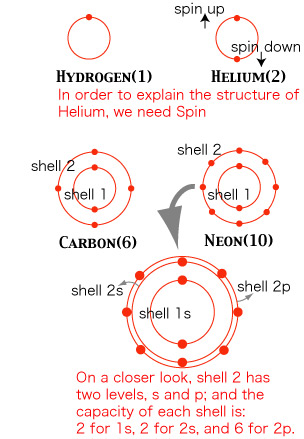
Let us have a glimpse of the atomic structure. Researches after the Bohr model of hydrogen revealed a remarkable structure. An atom has a number of layers of electrons---concentric shells, so to speak, if you wish to have a rough image---; and each layer has a different maximal number (capacity) of electrons allowed. These facts were revealed mainly by the analysis of spectra. For instance, hydrogen has only one electron, and in the normal state (called "ground state" with the lowest energy) it is located in the 1st shell; the next element Helium has two electrons, and both are located in the 1st shell---one electron has spin "up", and another "down". Let us illustrate some of the lighter elements (do not take the shape of the shell too seriously; in quantum mechanics, pictures in space and time does not make good sense).
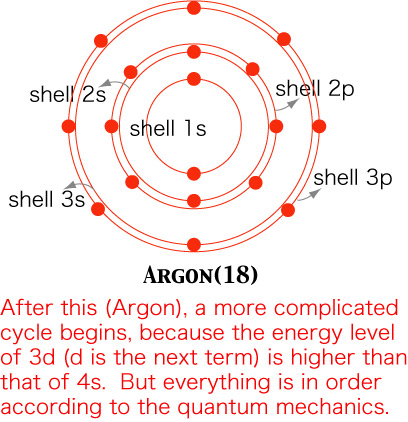
One more example, argon, which is another stable element. After argon, a complicated cycle begins, because the energy level of 3d (d is the next term, and f follows; the capacity of each is 10 and 14, respectively) is higher than 4s.
Later, it turned out that an important principle is working here. Each different trajectory of electron, taking the different spin into consideration, has the capacity of exactly one; if it is occupied by one electron, another can never enter. This is Wolfgang Pauli's Principle (1925). Why 1s or 2p etc. has the capacity it has, can be beautifully explained by this principle. Thus, a single shell in the preceding figures are actually a cluster of different trajectories. That is, in Helium, for instance, two different trajectories are located in shell 1s, and each is occupied by a single electron.
By the way, the integral numbers which appeared in the preceding diagram (s, p, e, f etc. are included, since they are abbreviations of such numbers) are what is called "quantum number"; they work in combination, as you have already noticed. Quantum mechanics essentially involves such numbers, unlike the classical mechanics. To be more specific, the quantum number appears in the following four aspects: (1) trajectories of electron around the nucleus (only a limited number of trajectories are allowed, and there are "quantum jumps" among them); (2) the angular momentum (e.g., that of an electron essentially involves an integral number); (3) azimuthal quantization (e.g., the plane of a trajectory of an electron can have only a limited number of directions); and (4) the spin, already mentioned. See the following diagram (adapted from Rom Harre's Great Scientific Experiments, Phaidon Press, 1981, Fig. 123).
Rom Harre (1981) Great Scientific Experiments, Phaidon Press (邦訳、『世界を変えた20の科学実験』小出昭一郎・竹内敬人・八杉貞雄訳、産業図書、1984)
Tomonaga, S. (1969) 量子力学 I、みすず書房。
See also a useful site on Microphysics, at Kyushu University: http://www2.kutl.kyushu-u.ac.jp/seminar/MicroWorld/MicroWorld.html