

Energy Quantum
Planck discovered a formula for the hollow-space radiation: this formula covered Rayleigh-Jeans formula and Wien's formula as a special case, where they fit well with experiments; and thus Planck's formula gave experimentally satisfactory results. Not only that, Planck also proposed a reason why such results follow with respect to the hollow-space radiation.
Planck's idea is something like this. If we suppose that energy can be distributed continuously, we cannot reach experimentally satisfactory formula, as was shown by Rayleigh-Jeans and Wien's formulae. However, if we may suppose that energy can be distributed only discretely, in an indivisible unit (like an atom), then we can reach the preceding satisfactory formula for the hollow-space radiation. In a word, by extending Boltzmann's method of Atomistic to radiation, we can have a theory of energy distribution in radiation. Thus emerged the notion of "energy quantum" (Planck 1901).
A wave with frequency ƒË can have energy E according to the following equation (n is an integral number, and h is Planck's constant), and this constrains energy distributions:
E = nhƒË
With this hypothesis of energy quantum, the distribution of energy to radiation with smaller or larger capacities (determined by kT, where k is Boltzmann's constant and T is temperature) may be illustrated as follows:
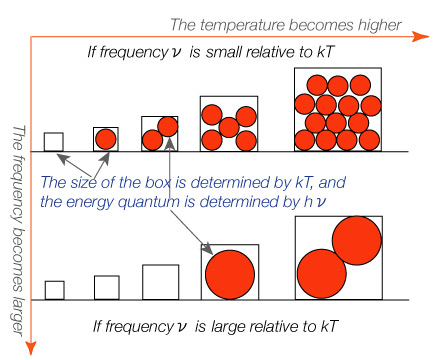
Then, how does this affect the amount of total energy in the hollow-space? You can grasp the significance intuitively, with the aid of the following figure (by adapting Dr. Tomonaga's Figure 11).
Planck, M. (1901) "Ueber das Gesetz der Energieverteilung im Normalspectrum", Annalen der Physik (4) 4, 553-563 (1901).