満室のトイレ

テナントビルのとある1フロア、トイレの混雑が目立つ。

社員、派遣社員等含めて200名くらい、男性に限ると170名くらいか。

この人数にトイレの個室は3つ。満室で、我慢を強いられることもしばしば。
そんな中、「満室だったので上のフロアへ行ったら、そこも満室だった」という話を聞いた。

胸が詰まりそうになった。

トイレも詰まりそうだ。

それにしても、上のフロアは半分は会議室ゾーンで追加人員は少ない。170人とはいえ6部屋も詰まるとは？
涙をこらえながら(決して笑いをこらえながらではない)、計算してみた。

前提条件は、

• 通常勤務の8時間(480分)中、催す確率は均一。(乱暴な仮定)
• 170名に個室は3つ。(リアル)
• 大きい方を催すのが、2日に1回。0.5回/日。(こんなもんか)
• 1回あたり3分の所要時間とする。つまり、単位時間に催す確率は、0.5×3/480。

まず、一番単純にやってみる。
3人以上が同時に催したときに満室になるわけだが、3人同時の確率は、

(0.5×3/480)³

その3人の組み合わせの数は、₁₇₀C₃通りあるので、

₁₇₀C₃×(0.5×3/480)³=0.025

となる。約2.5%だ。
残りの167人が催していようが催していまいが関係ない、4人同時だろうが5人同時だろうが満室は満室、とするところがドンブリである。

所要時間の3分は比較的すんなりいったときのこと。実際はもうちょっと長いかもしれないが、実測はしていない。こてPだから。
ちなみに所要時間が4分になると、確率は倍以上の約5.8%にもなる。
籠もるのは罪である。

さて、もう少しリアルに考えてみる。
上の計算では、4人同時、5人同時のケースも含まれるが、不幸にして4人目になった人がそのままあきらめるとは思えない。

出直しがあるはずだ。いや、この場合出し直しか、、、。まぁいい。
つまり、出(し)直せば、出(し)直した人が再び満室に寄与する可能性があるから、もうちょっと確率が上がるといういことだ。

いったんあぶれた人が、別の時刻に訪れることによって満室になる確率を2.5%に加えてやる必要がある。
たとえば、4人同時ケースが生じ、あぶれた1人が後で2部屋使用中に訪れる確率である。

4人以上ではなく、4人だけが同時の確率だと、残り166人は催していてはいけないから、確率は、

(0.5×3/480)⁴ × (1-0.5×3/480)¹⁶⁶

4人の選び方を考慮するとこうなる。

₁₇₀C₄ × (0.5×3/480)⁴ × (1-0.5×3/480)¹⁶⁶ = 0.002 ‥‥(1)

あぶれた人の出(し)直し時に2室占有の時に満室となるが、2室占有の確率も同様に、

₁₇₀C₂ × (0.5×3/480)² × (1-0.5×3/480)¹⁶⁸ = 0.083 ‥‥(2)

これらが同時に起こるので、

(1)×(2) = 0.0002

となる。0.02%。
3人以上とザックリ考えた2.5%に比べて追加分の0.02%は、ゴミみたいなものである。

体感的に、2.5%というのは小さい気がする（もっと3部屋満室には遭遇する気がする）のは、行きたくなる時間帯はみんな同じ、ということだろう。
平均するといい線いってる気がする。

さらに、5人同時ケースであぶれた2名が、別々に2部屋使用中に訪れるケースや、あぶれた2名が1部屋使用中のところへ同時に現れるケースなど、考え出すと大変複雑に見えるが、考え方は同じだ。

ゴミである。

さて、ドンブリの精度が意外に使えることがわかったところで、2つのフロアであぶれた冒頭の彼の経験がどれほど貴重なものかを計算してみる。

2フロアのトイレ6室を満室にしているのは6名であるが、この場合は当人も難民状態であるから、7名同時ケースである。
また、満室にしている6名は、彼をのぞく169名の中の組み合わせであるから、

₁₆₉C₆×(0.5×3/480)⁷=8.6×10^-8

0.0000086%。なんと1000万回に1回の確率。

所用時間を1回あたり4分にしても、155万回に1回の運のなさ。
大丈夫か？

さて、せっかくなので、170人いるところでの3室が満室になる確率が、一人当たりの所要時間でどう変わるのかを載せておこう。

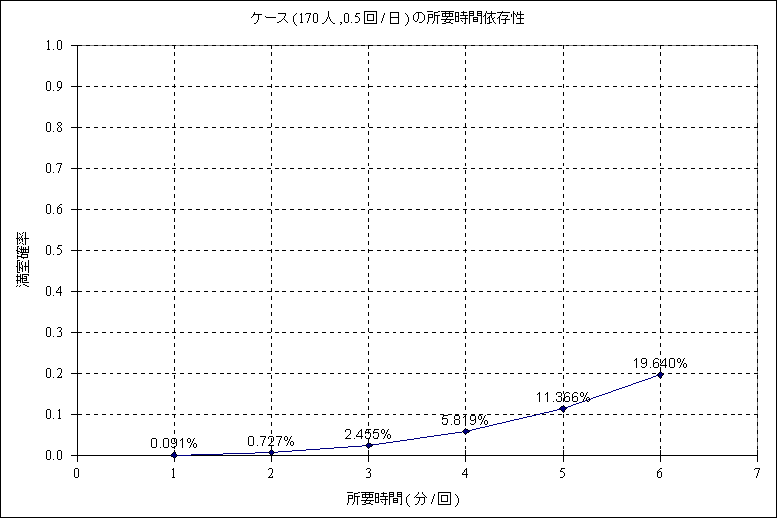
みんな、早く済まそうね。(←これが言いたかった。)