|
科学哲学ニューズレター |
![]() No.15, September 1996
No.15, September 1996
S. Uchii, "Laplace against the French Lottery"
ラプラスは富くじに反対!(内井惣七)
今年の学部演習では
Laplace, Essai Philosophique sur les Probabilite, 1814
を取り上げて読んでいる。これは、確率論における彼の主著
Theorie Analytique des Probabilite, 1812
の姉妹編とも言うべき、「インフォーマル」な解説であり、そのため彼の確率論のエッセンスを数学抜きで手っとり早く把握するのに便利な著作だと普通考えられている。しかし、実際にこの本を20ページほども読み進んでみれば、この甘い考えは大間違いであることがわかる。数式抜きの確率論は数式だらけの確率論よりもかえってむずかしいのである!筆者はこの夏悪戦苦闘してこの本(初版)の邦訳(第一次稿)を終わりにまでこぎ着けたが、最大の難所は「確率計算における解析的方法について」という14ページほどの一節であった。これだけの短いスペースのなかに、順列組み合わせの計算から始めて、差分方程式、数列と級数の理論、母関数の理論、それに関連した微分と積分の話がまったく数式なしのフランス語の散文で「解説」されているのである。結局、文意を把握するためだけでも『解析的理論』の該当する箇所を捜し当てて数式の意味をまず理解しなければ、意味の通る翻訳など不可能である。

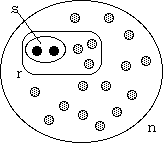
愚痴はこれだけにして、以下では比較的やさしい数学で理解できる「フランス富くじ」の話を紹介してみよう。国家の財政をうるおすためのこの富くじは、1758年、ルイ15世の時代に始められ、ルイ=フィリップの時代、1832年まで続けられた(図を参照)。このくじは、90の番号から一回の抽選で5つの当たりくじが出るというものである。では、
(1)ある与えられた番号が一回の抽選で当たる確率はいくらだろうか。
これは初歩的なやさしい計算ですぐにわかる。すなわち、抽選が公明正大であれば、任意の番号が当たりくじになる確率は 5/90、すなわち 1/18
である。ところが、フランス富くじの当たりくじに対する配当は出資額(くじ券の代金)の15倍でしかなかった。つまり、1フラン出してくじを買って当たっても、15フランしか貰えないのである(純益は14フラン)。しかし、パスカル・フェルマ以来の「公平な賭」の原理によれば、くじや賭が公平であるためには、それに参加することの数学的期待値はゼロ(つまり、損得なしゆえ公平)でなければならない。しかし、フランス富くじの券を一枚買う(簡単のため1フランとしよう)ことの数学的期待値は、単純に貨幣の額で測ることにすれば、
(2)(当たる確率×当たりの利益)+(外れる確率×外れの損失)
=(1/18)×(15−1)− (17/18)×1=−(1/6)
となって、明らかにマイナスである。この期待値をゼロにするためには、配当の倍率はいくらでなければならないだろうか。配当をSフランとして、(2)式をしかるべく書き換えれば、
(3) (1/18)×(S−1)− (17/18)×1=0
となって、これをSについて解けば18となる。つまり、配当率は確率の逆数でなければならない。

以上のように、富くじの主催者は必ず儲けが出るように配当率を設定するのは世の習いであるが、大衆にくじの魅力をアピールするためにもっと工夫を凝らす。フランス富くじでは、二連勝(ambe)、三連勝(terne)、四連勝(quaterne)、および五連勝(quine)――すなわち、買った番号がそれぞれ二つ、三つ、四つ、そして五つとも当たること――の配当率が一見非常に魅力的に設定されたのである。
二連勝 270倍
三連勝 5,500倍
四連勝 75,000倍
五連勝 1,000,000倍
さて、これらの配当率が本当に魅力的かどうかを判断するには、かなりの数学的洗練を必要とする。例えば、
(4)与えられた(自分の買った)二つの番号が 二連勝となる確率はいくらだろうか。
この種の問題を解くときに数学の真の威力が発揮される。ラプラスは、フランス富くじだけでなく、任意の富くじの、任意の数の連勝の確率を計算できる定理を導き出す。その箇所を引用しよう。
(5)ある富くじはn個の数字からなり、毎回の抽選でr個の数字が取り出されるとしよう。このとき、s個の与えられた数字が一回の抽選で出る確率はいくらだろうか。この確率を得るためには、まず、一度にr−s個とる他の数字の組み合わせの総数を決めなければならない。なぜなら、これらの組み合わせの各々に与えられたs個の数字を加えると、n個の数字から一度にr個を取り出してその中に与えられたs個の数字が含まれている組み合わせの総数を得ることが明らかだからである。この数をすべての数字からr個を取る組み合わせの数で割ると、問題の確率が得られるであろう。かくして、この確率は、r個の数字から一度にs個を取る組み合わせの数が、n個の数字から一度にs個を取る組み合わせの数に対して持つ比率に等しい。
これはそれほどむずかしい定理というわけではないが、やはり組み合わせの記号なしでは理解すらむずかしい。高等学校で習った数学を想起していただいて、m個の異なるものからk個を取り出すときの可能な組み合わせの総数を
mCk と表記することにしよう。もちろん、
(6)mCk = m!/k!(m−k)! (m! = m(m-1)…1)
である。そうすると、(5)の推論のポイントは次のように解説できよう。
まず、s個の数字は与えられているのだから組み合わせの余地はないことに注意しよう。そこで、当たりくじr個のうち、組み合わせの余地があるのは残りのrーs個だけである。つまり、nーs個の数字からrーs個を選ぶ組み合わせの総数が、すべての可能性のなかで、与えられたs個の数字を当たりくじにする可能性の数であり、これが問題の確率を決める分数の分子に来る。分母は、当然与えられた条件のもとで可能なすべての組み合わせの数、つまりn個の数字からr個を取る組み合わせの総数である。そこで、(5)は結局次のようになる。
(7)n個の数字からr個を抽選する場合、与えられたs個の数字がそのr個の中に含まれている確率は、{(n-s)C(r-s)}/nCr = (rCs)/(nCs)
である。
この定理に従って二連勝以下五連勝までの確率を計算すると、
二連勝 10/4005 公平な配当は400.5倍
三連勝 1/11748 公平な配当は11,748倍
四連勝 1/511038 公平な配当は511,038倍
五連勝 1/43949268 公平な配当は43,949,268倍
となる。これと比べると、前述の実際の配当率がいかに低すぎるかわかるであろう。これを一つの理由として、ラプラスはフランス富くじには反対の意見を持っていたのである。
編集後記 本格的なフランス語の歴史的文献に取り組むのは、筆者の「学界デビュー」(?)当時のルソー研究(1967-1969)以来のことであり、錆び付いたフランス語力が心配されたが、自信に溢れた啓蒙主義者ラプラスのフランス語はそれほどむずかしくなく、むしろ数学の再構成の方に多大の時間を費やすこととなった。ラプラスの邦訳はすでに『試論』(抄訳)と『解析的理論』と二つあるのだが、筆者にとって最も参考になったのは最新のA.I.Dale の英訳(Springer, 1995、詳しい注がついている。伊藤和行助教授提供)である。『試論』に対する注釈は、I.Todhunter, K.Pearson, R.von Mises らの先人の仕事があるが、Daleはこれらを集大成した観がある。しかし、なお散見する誤りや不明瞭な点はいくつか改善したつもりである。(96.9.27/内井惣七)
Last modified Nov 29, 2008.
