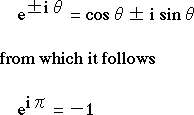Å@
Leonhard Euler (1707-1783)
One of the greatest figures in the 18th century. Laplace said, "Read Euler, read Euler. He is the master of us all." Euler was born in Basel, Switzerland, and studied under Johann Bernoulli. When Euler was 20 years old, he obtained a post in St. Petersburg Academy, Russia. Petersburg was stimulating , because there were a number of eminent scholars (Daniel Bernoulli, among others), and Euler was quite productive.
Euler was the first to give an analytical treatment (in terms of differential equations, not in terms of older geometrical method like Newton's) of mechanical problems, and he published Mechanica (1736-37). However, he lost the sight of the right eye, because of illness and strain. Then in 1741, he was invited to Berlin, where Frederick the Great established Berlin Academy (1744). During the 25 years in Berlin, he was again prolific and produced well more than 300 papers. During this period, he published a short paper in French, "Reflexions sur l'espace et le temps" (1748) criticizing the Leibnizian "metaphysical" view of space and time (as relations of things), which impressed Kant and made him reconsider the relation of physics and metaphysics. Euler argued that metaphysics must learn from physics, rather than criticizing physics in light of obscure principles of metaphysics, and metaphysicians should test their ideas in light of "established" principles of physics.
Euler after he lost the sight of the right eye
However, frustrated by the King's treatment (the King's taste was French, whereas Euler was a Calvinist), he left Berlin and went back to Petersburg in 1766. Soon after his return, he lost eye-sight completely, but continued to be productive thanks to his own prodigious ability and able assistants (he could perform complex calculations without pen and paper, and his memory was incredibly strong).
Euler made great contributions in many fields of mathematics, astronomy, and mathematical physics. To give just a single instance, Euler's formula combines, in a beautiful manner, trigonometrical functions and exponential functions by the mediation of imaginary numbers. A Japanese author published, several years ago, a book devoted to understanding and applying this formula:
Reference
As regards Euler's mathematical work, William Dunham's Euler: the master of us all, Mathematical Association of America, 1999 is compact and readable.