Boole's Symbolic Logic

Boole's Symbolic Logic

From The Laws of Thought (1854)

Boole and de Morgan began the modern symbolic logic, or the Boolean Algebra in other words. Here is some extract from Boole's 1854 book.

All the operations of Language, as an instrument of reasoning, may be conducted by a system of signs composed of the following elements, viz.:

1st. Literal symbols, as x, y, etc., representing things as subjects of our conceptions.

2nd. Signs of operation, as +, －, ×, standing for those operations of the mind by which the conceptions of things are combined or resolved so as to form new conceptions involving the same elements.

3rd. The sign of identity, =.

And these symbold of Logic are in their use subject to definite laws, partly agreeing with and partly differing from the laws of the corresponding symbols in the science of Algebra.

Thus, for example, if x and y represent two classes of things, respectively, x+y expresses a joint class of x and y, x×y or xy expresses the class of those things which belongs both to x and to y. And the identity (equation) x = xy expresses that the lefthand and the right hand of the equation refer to the same class.

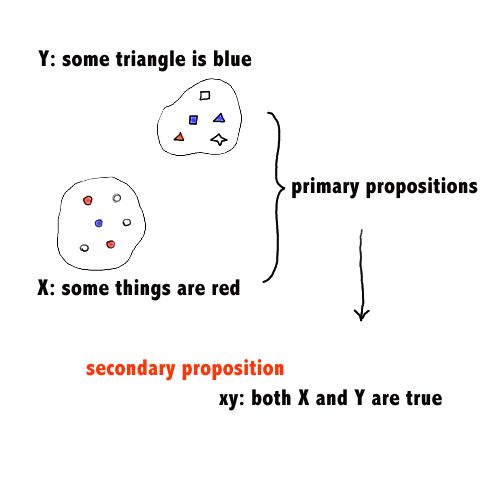
It should be noted that the same symbolism can be used either for (1) the propositional logic and for (2) the Aristotelian Syllogism, depending on the interpretation of symbols. In Boole's book, these are called the logic of secondary propositions and the logic of primary propositions, respectively. The names may seem strange, but the idea is that the proposition (e.g. Aristotelian categorical proposition) expressing the relation of things is primary, and Boole thought, in (1), a proposition is expressing truth or falsity of a primary proposition. Thus, e.g., xy means, according to this interpretation, that both a (primary) proposition and another (primary) proposition are true (see the figure). However, the contemporary logicians do not adopt this terminology; instead, they regard (1) as more elementary and fundamental than (2).