
The Principle of the Identity of Indiscernibles
Leibniz's Fourth Letter
Leibniz: "Those great principles of sufficient reason and of the identity of indiscernibles change the state of metaphysics. That science becomes real and demonstrative by means of these principles, whereas before it did generally consist in empty words."
The principle of the identity of indiscernibles is stated here as follows: To suppose two things indiscernible is to suppose the same thing under two names. But again, this principle, as it stands, allows ambiguity. Indiscernible on what criteria? Is this principle a priori or empirical (contingent)? Leibniz sometimes speaks of "indiscernibility in terms of intrinsic qualities" or "no internal differences", but this does not entirely eliminate ambiguity. Moreover, Leibniz's notion of "individuals" is defined in a peculiar way (we will not get into this) so that an individual and the (possible) universe which contains it may be inseparably connected (according to Dr. Matsuou who wrote a thesis on Leibniz's possible universes some 10 years ago).
In the Fifth Letter, Leibniz seems to commit himself to the version of this principle which is not a logical principle:
When I deny that there are two drops of water perfectly alike, or any two other bodies indiscernible from each other, I do not say it is absolutely impossible to suppose them, but that it is a thing contrary to the divine widsom, and which consequently does not exist. (Fifth Letter, 25)
Then, we can interpret that this is a posteriori principle, containing some substantive content. In our modern terminology, whether this principle is true or not depends on the nature, the laws of nature. Then whether or not the Newtonian atomism is true becomes an empirical question. And since Leibniz sometimes says that this principle follows from that of sufficient reason, the same remark holds for the latter too. Let us keep this in mind.
However, despite these misgivings, this principle of indiscernibility does have a significance in modern physics. A good example is statistical mechanics, which treats macroscopic properties of a large set of particles. The point is, depending on what kinds of particles you are talking about, the criterion of identity of a state (i.e. a microscopic state) may differ. Although all this presupposes the "corpuscle" picture of matter which Leibniz did not like, the significance of Leibniz's principle may be somehow defended.
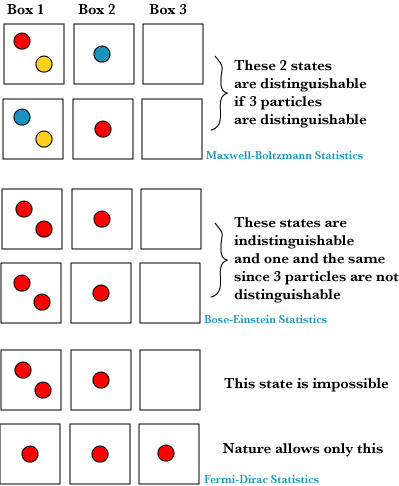
To make things easier, suppose there are three different boxes which can contain a certain number of particles; to make things much easier, we may suppose there are only 3 particles. Then, a priori, each box can contain either 1, or 2, or 3 particles. However, our Mother Nature may not be as simple as this! But if we count all possibilities of distributing the 3 particles to the 3 boxes on this supposition, the result is the Maxwell-Boltzmann Statistics. See the following Table 1:
This statistics presupposes that the three particles are distinguishable from each other; e.g. one is red (R), the second is blue (B), the third is yellow (Y), for instance. Thus looking at the fourth row, Box 1 may contain either (1) R and B, or (2) R and Y, or (3) B and Y; hence there are 3 possibilities. This statistics is valid for the kinetic theory of gases; this regards a gas as a large collection of molecules, and each molecule is distinguishable from each other, just as a red ball is distinguishable from a blue ball, however they may be similar in other respects.
Next, suppose all of the 3 particle have the same color, say R; then any pair is indistinguishable (although you can say there are 2 particles) . On this supposition, we obtain a different table, Table 2:
This is in essence the Bose-Einstein Statistics. This statistics is valid, for instance, for a collection of photons, and this means that photons are indistinguishable: they do not have any such individuality as a red ball or a blue ball or gas molecules (but still you can count photons, one, two, three, etc.). So far, some of Leibniz's contentions, e.g. that there are no two indistinguishable things, seems to be refuted, if you concentrate on the particles. However, if you pay attention to the states, Leibniz seems to be right! For instance, look at the fourth row again. Since Box 1 contains two particles, you may think there are 3 different ways to choose 2 from 3 particles; but the answer is NO, maybe to your surprize! There is only 1 way, because 3 particles are indistinguishable!
But this is not the end of the story yet. Suppose next that, for some reason, each box can contain only one particle. Then clearly we have the following table, Table 3:
This means that the state, in the sense of a distribution of particles to each box, is uniquely determined, as well as that each particle is indistinguishable. Do you think that such a weird thing does not exist in nature? Wrong! As I have already explained in Bohr Seminar, this is nothing but Pauli's Principle, and the statistics of Table 3 is the Fermi-Dirac Statistics. Here, Leibniz's contention becomes valid! The electrons in an atom (such as Hydrogen, Helium, etc.) is constrained as severely as this. Notice also that in Monadology, Leibniz speaks of the differences among the monads (simple and ultimate substances) in terms of their states, which are determined by their relationships; these relationships are nothing but the ways those monads perceive the others, the ways they mirror the others. See Monadology.
The following Figure summarizes all this:
For another example of the revival of Leibniz's principle of indiscernibility, the "Hole Argument" in the general relativity is well known. The point is that we have to distinguish between mathematical identity and physical identity, when it comes to any solutions of Einstein's equation of gravitational fields. Two mathematically distinct solutions are nevertheless indistinguishable as a physical process, and the general relativity is historically the first instance of a theory of physics, which allows this. Leibniz's ideas have this long range! See this.
Last modified, June 30, 2005. (c) Soshichi Uchii